Polígonos estrellados en Matemáticas 2

Haciendo un poco de historia, Pitágoras fundó una sociedad de conocimiento:

Al construir una circunferencia cualquiera, y se dividen en partes iguales y se unen los puntos de división de dos en dos, de tres en tres, etc., y al cerrarse la poligonal ha recorrido la trayectoria de la circunferencia un número n/p,  donde:

n, corresponde al número de vértices del polígono regular convexo

p, es el número de saltos entre los vértices

Otra característica es que p debe ser un número menor que la mitad de n, además debe ser un primo relativo con n, es decir, una fracción como 5/2 debe ser irreducible o bien tener como divisor común la unidad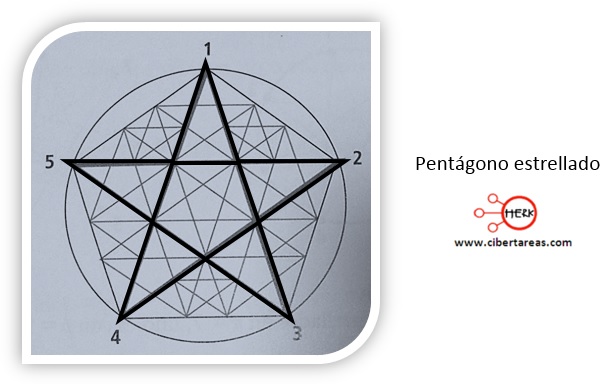

Ejemplo

-Se tienen un heptágono y su cociente es: 7/2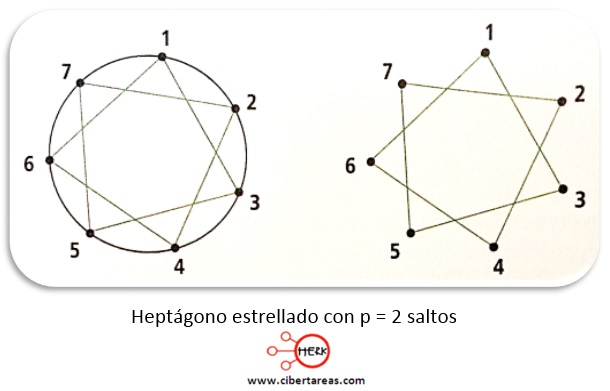

 -Es necesario que se exhiba modo de figuración

-¿Cuántos polígonos estrellados se forman?

Solución

-Datos

-Fórmula general: n/p

-n = 7 vértices

-p = 2 saltos entre vértices

-Es necesario buscar al menos un polígono estrellado

Análisis

-Para obtener un heptágono estrellado cada 2 saltos, primero se traza una circunferencia y se  dividen los 360° en 7 partes iguales

-Se unen las puntas con un segmento de recta dando dos saltos, si se inicia en 1, luego de dos vueltas enteras se llega a este mismo punto

-La secuencia sería:

-De 1 a 3

– De 3 a 5

-De 5 a 7

-De 7 a 2

-De 2 a 4

-De 4 a 6

-De 6 a 1

Al definir una razón de 7/3, en el heptágono los saltos se dan de 3 en 3, como se muestra en la siguiente figura: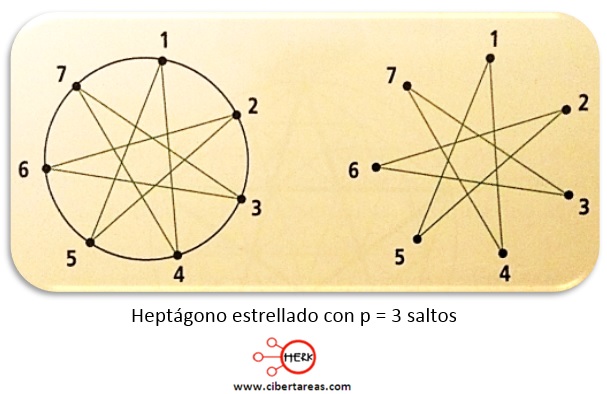

-Al iniciar en 1, luego de tres vueltas enteras se llega al mismo punto

-La secuencia será:

-De 1 a 4

-De 4 a 7

-De 7 a 3

-De 3 a 6

-De 6 a 2

-De 2 a 5

-De 5 a 1

Síntesis interpretativa

-Hay dos polígonos estrellados en n = 7, uno es con p = 2 y el otro con p = 3