Variaciones en las producciones máximos y mínimos relativos en Calculo Diferencial, donde la derivada siempre es horizontal por lo tanto es igual a cero.
Existen métodos más exhaustivos que nos garantizan encontrar dichos [Máximos y Mínimos] de una función a partir de funciones con valores extremos donde la derivada no es cero o bien donde la derivada en un punto de una gráfica sea igual a cero y la función no sea un valor máximo o un valor mínimo.
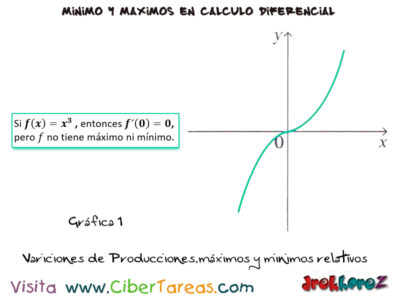
1.- Si f(x)=x3 entonces f'(0)=0 pero f no tiene máximo ni mínimo.
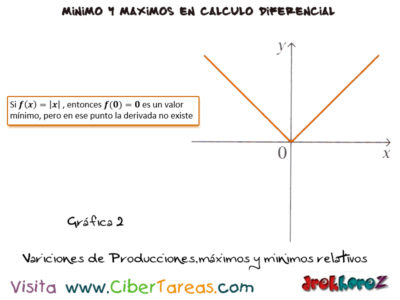
2.-Si f(x)=|x| entonces f(0)=0 es un valor mínimo, pero en ese punto la derivada no existe.
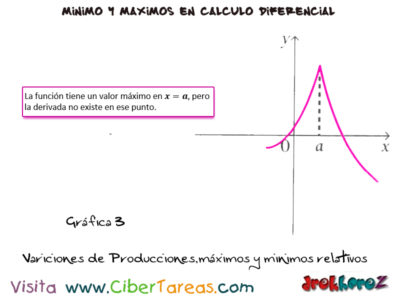
3.-Esta función tiene un valor máximo en x=a, pero la derivada no existe en ese punto.
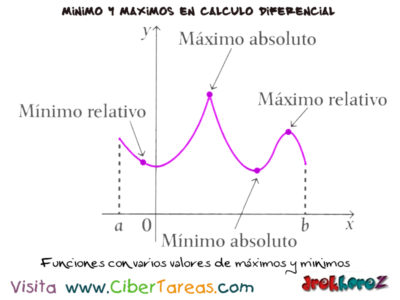
Una función f posee un máximo local [o máximo relativo] en un valor crítico c si f(c)≥f(x) cuando x está cercano a c. De la misma manera, f tiene un mínimo local o minio relativo en c si f(c)≤f(x) cuando x está cerca de c.
Una función puede tener uno o más valores máximos o mínimos relativos en un intervalo (a,b) pero sólo un máximo absoluto mayor que todos y un mínimo asoluto menor que todos o solo alguno o ninguno de los dos.