Aceleración centrípeta (radial) en Física 1
Aunque la velocidad lineal no sea constante en el movimiento circular uniforme, implica que debe existir una aceleración
Como la magnitud de la velocidad tangencial es constante, la aceleración no es colineal con dicha velocidad, sino perpendicular a ella, en consecuencia, en el movimiento circular uniforme (MCU) la aceleración está dirigida siempre hacia el centro, por lo que se llama centrípeta, este término fue acuñado por Isaac Newton y significa que busca el centro, como se muestra a continuación: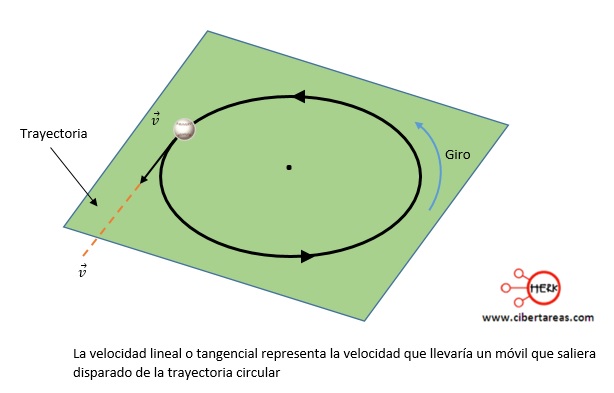
Para determinar la magnitud de la aceleración centrípeta podemos considerar un móvil que tiene un movimiento circular uniforme y cuyas velocidades en dos posiciones se muestran a continuación: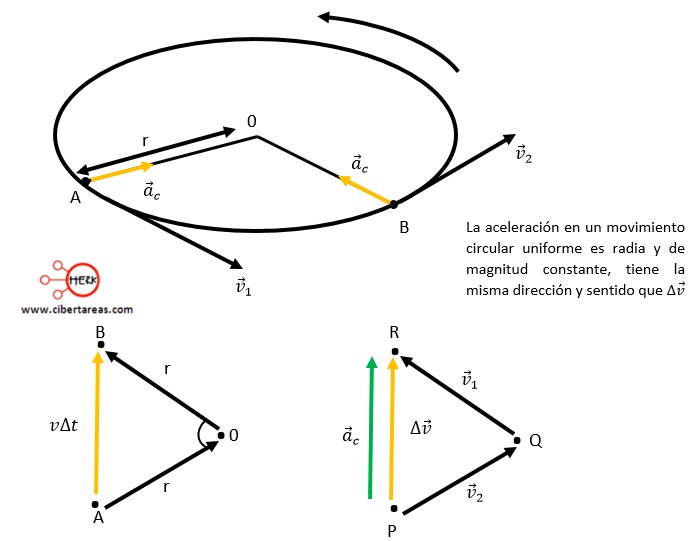
Ya que la aceleración es igual a 
de las velocidades en las dos posiciones (punto A y B)
Conforme al intervalo de tiempo se hace más pequeño 
Al considerar que el intervalo de tiempo 
entre los puntos A y B es muy pequeño, la longitud del arco de la circunferencia entre dichos puntos es prácticamente igual a la longitud de la cuerda entre los puntos A y B
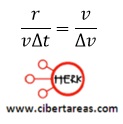
Por lo anterior, al hacer un análisis de la imagen anterior, de los dos triángulos semejantes OAB y QPR de la figura anterior, se obtiene: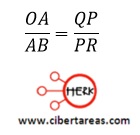
Como 
, entonces:
Reordenando la ecuación se obtiene:
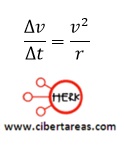
Ya que ∆v/∆t representa la magnitud de la aceleración (también conocida como aceleración centrípeta) ac, entonces: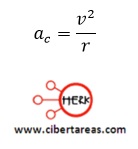
La unidad e la aceleración centrípeta en el SI es el m/s2
Ejemplo del cálculo de la aceleración centrípeta
-Problema:
-Una pelota atada a una cuerda gira en círculo de radio r = 1 m con una rapidez lineal constante de 4 m/s
-¿Cuál es el valor de su aceleración centrípeta?
-Solución
-Datos
v = 4 m/s
r = 1 m
ac = ?
-Formula
-Sustitución
-Resultado
ac= 16 m/s2
