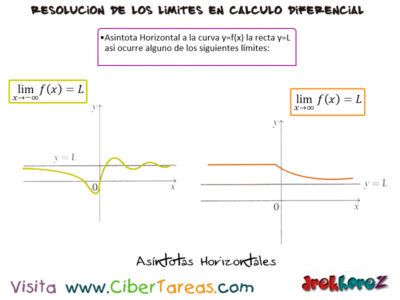
Asíntotas Horizontales en el Cálculo Diferencial se le llama a la curva y=f(x) la recta y=L si ocurre alguno de los siguientes limites:
Podemos apreciar en las siguientes gráficas de la imagen:
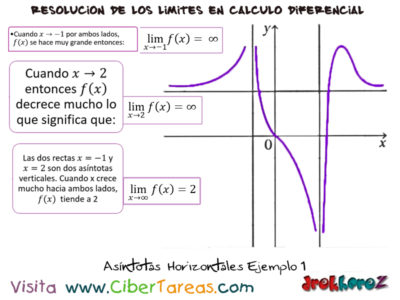
En un ejemplo claro podemos apreciar cuando x–>-1 por ambos lados f(x) se hace muy grande entonces, cuando x–> 2 entonces f(x) se decrece mucho lo que significa que:
El cual concluimos que pues las dos rectas x=1 y x=2 son asíntotas verticales cuando x crece mucho hacia ambos lados, f(x) tiende a 2.Asi entonces significa que y=2 es una asíntota horizontal.
Un ejemplo claro que es común como asíntotas es y=1/x dado que si calculamos por ambos lados de 0 lo que tenemos en la siguiente imágenes.
Si lo exploramos vamos encontrar lo que muestra que tanto el eje x como el eje y son asíntotas horizontal vertical respectivamente.
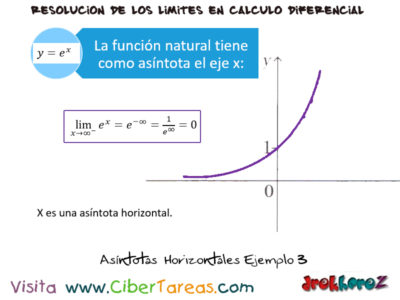
La función natural y=ex tiee como asíntotas el eje x a partir de la gráfica y unas cuantas operaciones básicas podemos concluir lo siguiente:
Por lo tanto x es una asíntota horizontal en la siguiente imagen: