Derivada como Razón de Cambio Instantánea en el Calculo Diferencial.En una función [F], es otra función denotada por [F´] y definida mediante:
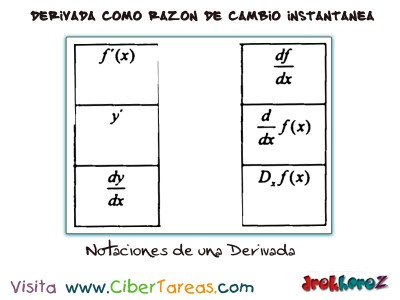
Ya que la derivada de una función: es el limite de la razón de cambio instantánea.Aclaramos que existen algunas otras notaciones para la derivada como:
Ya que la Expresión [d/dx] expresa que debe tomarse la derivada con respecto a [x] de cualquier expresión que siga.



Maru Pérez says:
Me podrían ayudar a resolver estas derivadas en razon de cambio:
a) f(x) = 8
b) f(x) = -6x
c) f(x) = -4x + 9
d) f(x) = -5/3x +4
e) f(x) =-5×2 -10
f) f(x) =-2×4 -6×3 -x2 +3
g) f(x) = -x+1 / x-1
h) f(x) = 1 /6×4
Maru Pérez says:
también necesito que me ayuden a resolver este problema:
Si la arista de un cubo crece a razón de cambio de 5 cm por cada segundo. ¿A qué velocidad cambia el volumen del cubo en el instante en que la arista mide 8 cm?
– Realiza una imagen de la figura
– Analiza lo que significa arista
– Coloca la fórmula del volumen para dicha figura
– Calcula utilizando derivadas
Por favor es urgente
Ricardo says:
revisa este video y te va aservir para resolver el problema.
https://www.youtube.com/watch?v=Mzq_0WGBtSo
Leticia VALADEZ says:
Solicito de su apoyo para responder este problema
Supongamos que el costo de la producción en pesos de x toneladas de jitomate está dada por la siguiente función: c (x) = 5×2 + 3x
Es decir, para producir 1,150 toneladas de jitomate se necesitan c (1,150) = 5 (1,150)2 + 3(1,150) = 6,615,950 (seis millones seiscientos quince mil novecientos cincuenta pesos).
Si queremos saber cuánto se deberá pagar si se incrementa la producción a 30 toneladas más, hay que derivar la ecuación de la producción total y así obtener el costo del incremento de la producción. Para ello, se puede realizar el siguiente proceso:
Se deriva la función del costo de producción
c(x)= 5×2+3x
Para derivarla se utiliza la siguiente fórmula, que es para realizar una derivada de un polinomio:
\small \frac{dx^{n}}{dx} = nx ^{_{n-1}}
El resultado o la derivada de la función de producción total es:
\small \frac{d[5x^{2} + 3x]}{dx} = 2 * 5x^{2-1} + 3 = 10x + 3>
2. A partir de lo anterior, responde:
• ¿Cuánto deberá pagarse por aumentar a 30 toneladas la producción, es decir, por producir 1,180 toneladas de jitomate?
• En esta situación ¿para qué se aplicó la derivada de la función de producción total?
Graciela Lombardo says:
Hola Leticia:
Aquí debes utilizar el concepto de diferencial de una función, el cual es una aproximación del incremento de la función.
Recuerda que el diferencial es:
dy=f'(xo). ∆x
Espero te haya sido útil mi comentario
Saludos
Graciela