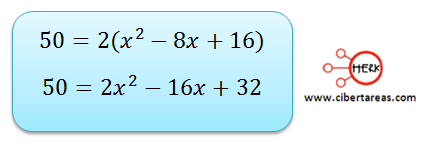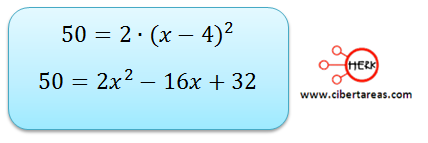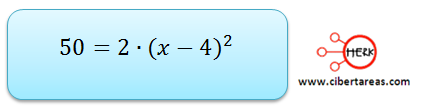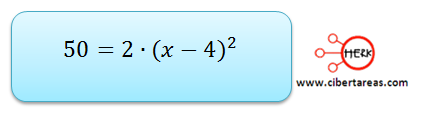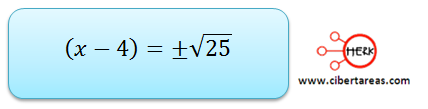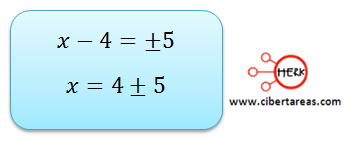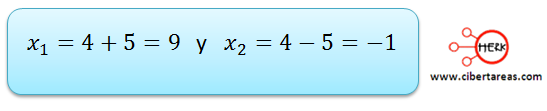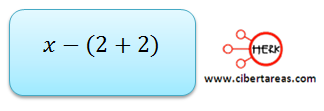Ecuación de segundo grado – Matemáticas 1

Estos ejemplos son aplicados en la vida cotidiana, con esto veremos la aplicación práctica de las ecuaciones de segundo grado.

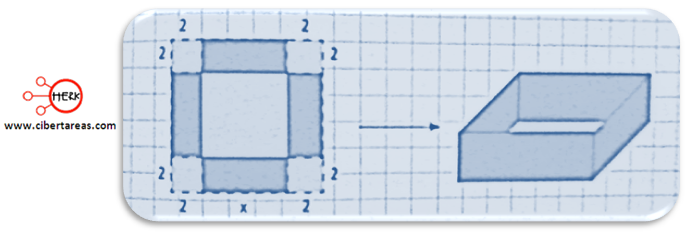
Se necesita construir una cada de 50 cm³ de volumen con una cartulina cuadrada, para esto, en las esquinas de la cartulina se cortan cuadrados de 2 cm de lado. ¿Cuánto mide cada lado de la caja?

Veamos la solución, tomemos una cartulina cuadrada, con una longitud x en sus lados

Procedemos a cortar cuadros de 2 cm de lado, doblando los lados de la cartulina como lo podemos observar:

Con estos cortes, podremos obtener una cada de cartulina con las siguientes dimensiones:

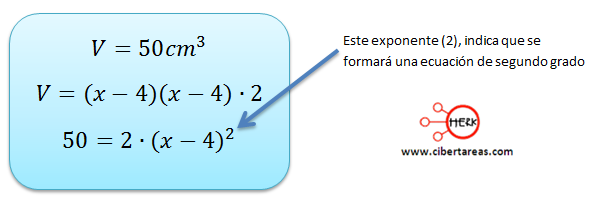
Cuando utilizamos la fórmula del volumen, se encuentra el valor de x

Desarrollando el binomio tenemos que:

Entonces tenemos que las siguientes ecuaciones son equivalentes:

Pero para resolver este problema vamos a utilizar la siguiente ecuación:

Primero, vamos a despejar a incógnita x:

Utilizando la propiedad de la igualdad dividimos entre 2 cada extremo de la ecuación:

Posteriormente se despeja el exponente:

Cuando se obtiene el producto de la raíz y al despejar la incógnita, se encuentran dos posibles soluciones:

Al realizar una síntesis interpretativa, podemos demostrar que una ecuación de segundo grado implica dos soluciones:

Para esta ecuación las dos posibles soluciones satisfacen la igualdad, pero no el problema

Primero debemos de demostrar que igualdad se cumple para ambos casos:

El lado de la caja se obtiene a partir de:

Cuando se sustituye x₁ se encuentra la respuesta:

Con esto se concluye que cada lado de la caja mide 5 cm.

Si observamos las posibles soluciones, podemos decir que no es posible que x₂ sea la solución a la ecuación, porque no existen distancias negativas.