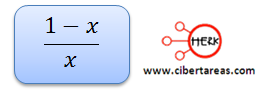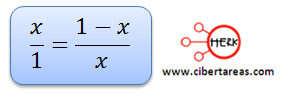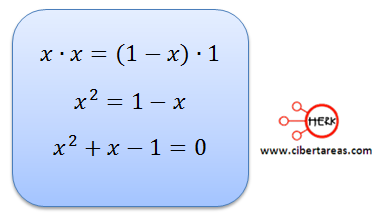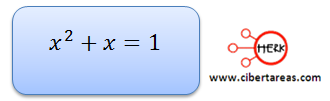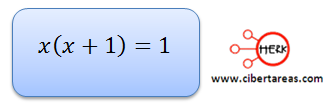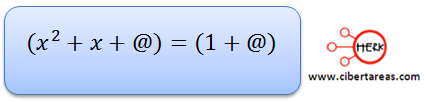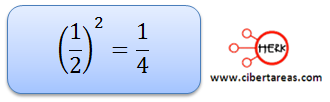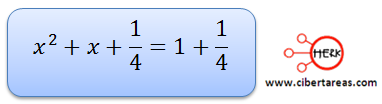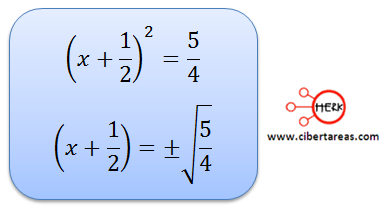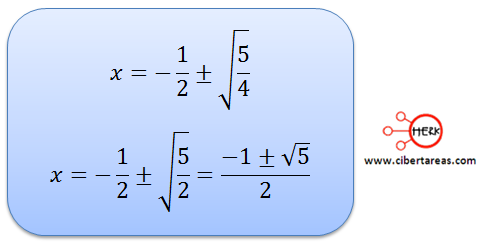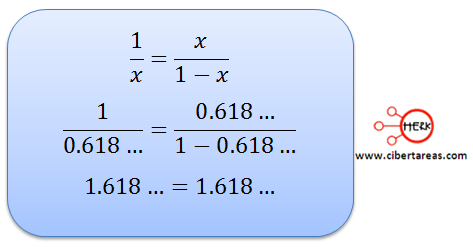Ecuaciones cuadráticas – Matemáticas 1
Vamos a analizar un problema para comprender de mejor manera las ecuaciones cuadráticas:
Dado un segmento de longitud uno, debemos de encontrar un punto que al ser dividido en dos cumpla una relación, que es la siguiente:
Esta relación nos indica que encontraremos la proporción áurea de un segmento.
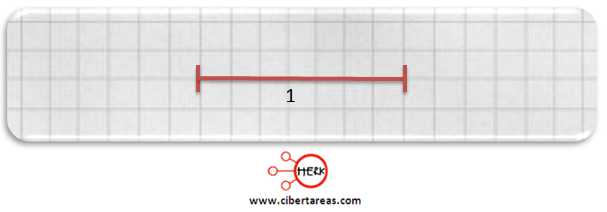
Primero trazaremos una línea que represente una unidad:
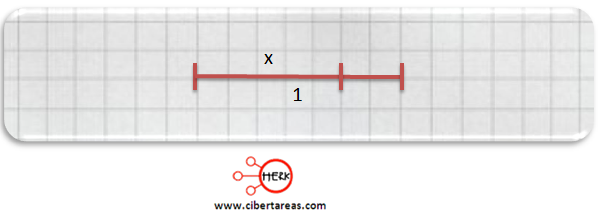
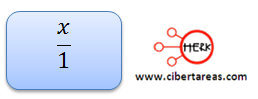
Segundo, es necesario determinar una distancia “x” para encontrar el punto de división, éste es el segmento mayor
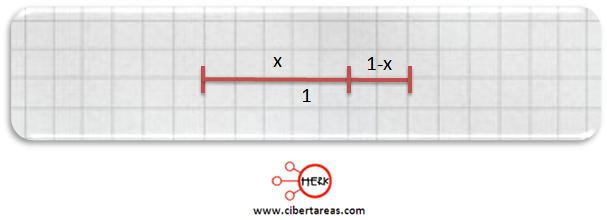
Tercero, ya se conoce el segmento de longitud 1, el segmento mayor y en este punto se puede deducir cuál es el segmento menor
Ahora establezcamos algebraicamente ambas relaciones:
Relación entre el segmento mayor y la longitud total
Relación entre el segmento menor y el mayor
La problemática de este ejemplo nos dice que estas dos proporciones deben ser iguales
Para poder definir se es cierta esta igualdad, debemos de encontrar el valor de “x”, entonces despejemos la incógnita
Con esta ecuación, se puede ver la forma de una ecuación de segundo grado o cuadrática.
Vamos aplicar un mecanismo que permita establecer una formula genera de solución, para esto se debe despejar la incógnita
La Factorizar no llegamos a un resultado, ya que el interés es despejar de manera natural la “x”, la expresión resultante es:
Para despejar “x” se utiliza el trinomio cuadrado perfecto (TCP)
Se puede observar que al primer miembro de la igualdad (x2+x) se le aumenta un término, se forma un TCP.
Se puede alcanzar la expresión inicial
Ahora, por las propiedades de la igualdad definiremos el valor de @
n esta ecuación el coeficiente del término intermedio es de 1 y es el doble de un número (1/2), pero para llegar a una ecuación TCP debe ser al cuadrado, por lo tanto el valor de @ es:
Si aumentamos este término a cada miembro de la igualdad tendremos:
Observemos que el lado izquierdo de la igualdad tiene un TCP completo, es la primera fórmula notable, mientras que en otro extremo simplificamos la suma al obtener el denominador común
Posteriormente de estos pasos es posible despejar de manera natural la incógnita “x” y hallar las dos soluciones:
Interpretando el problema, tenemos que: elegimos únicamente el valor positivo de la raíz, porque no tendrá sentido el valor negativo ya que no existen distancias negativas, entonces tenemos que:
Esta es la distancia que permite encontrar el segmento en proporción áurea.
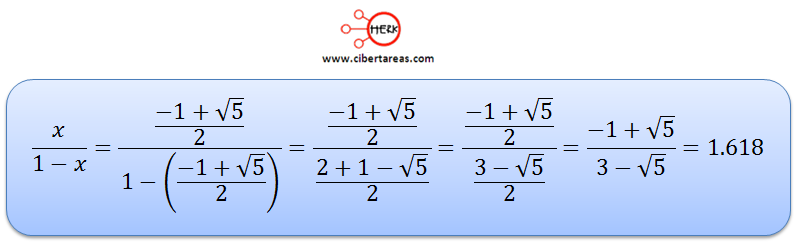
Al sustituir el valor de “x” en la siguiente expresión podremos hallar este concepto.
De este modo vemos como la razón áurea se comprueba y se obtiene si tomamos un segmento cualquiera y lo dividimos en dos partes, de tal manera que la razón entre la totalidad del segmento y la parte mayor sea igual a la razón entre la parte mayor y la menor, podemos demostrar el ejemplo:
Este valor que obtenemos es motivo de curiosidad o enigma ya que las aplicaciones y los lugares donde puede aparecer puede ser motivo de su estudio o un tratado.
El nombre de este “numero” es: