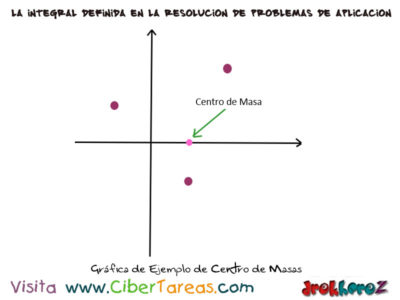
Ejemplos sobre el Centro de Masa en Cálculo Integral, al encontrar el centro de masa del sistema de partículas que tiene masas 2,4 y 9 en los puntos (-1, 1), (2, 2) y (-1, 1):
Primero calculamos los momentos de Masa (My Mx), la masa del sistema es m=2+4+9=15 y las coordenadas de centro están, por lo tanto del centro de masa está así se aprecia gráficamente:
De manera análoga se puede concluir que al igual que para un sistema de partículas, el centro de masa de una placa situada en el plano de densidad uniforme [r], masa [m] y área [A] [llamada centroide] se calcula con las siguientes expresiones:
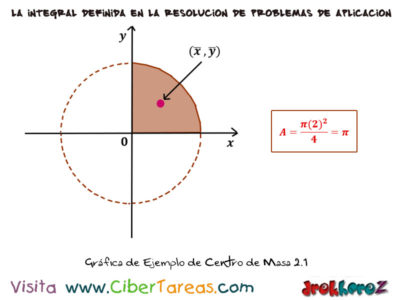
Ejemplo 2 , al encontrar el centro de masa de una placa que tiene forma de la forma de la cuarta parte de una circunferencia de radio 2 y que esta ubicada en el primer cuadrante.
Al colocar el plano cartesiano y recordamos que la ecuación de una circunferencia. Al despejarlo en la ecuación anterior tenemos que la función necesitamos:
El área de la región es la superficie de la circunferencia entre 4 es decir, que entonces las coordenadas del centro de la masa así están. Logramos calcular que por la simetría es evidente como se muestra en la figura anterior.