Los Límites en el Infinito en Cálculo Diferencial, al permitirnos que x se vuelva grande a nuestro arbitrio “Positiva o Negativa” e investiguemos qué le ocurre a y.

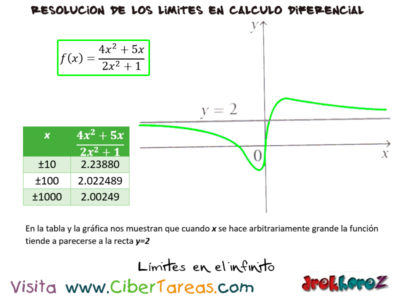
Comencemos explorando con el comportamiento de la función f(x) definida por la expresión. Vamos a observar la siguiente gráfica de la figura siguiente nos muestran que cuando x se hace arbitrariamente grande la funcionan tiende a parecer a la recta y=2.

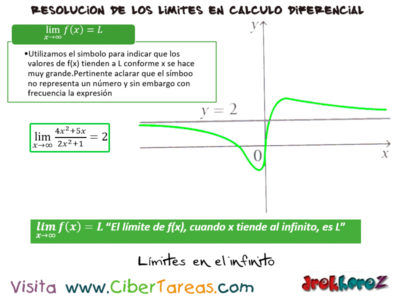
En la gráfica podemos apreciar que conforme a x crece más y más, los valores de la función se aproxima cada vez más a 2. Al generalizar un experimento como el anterior podemos utilizar el símbolo, para indicar que los valores de f(x) tienden a L conforme x se hace muy grande.

Esto permite aclara que el símbolo no representa un número y sin embargo con frecuencia la expresión se le como:

“El límite de f(x), cuando x tiende al infinito es L”