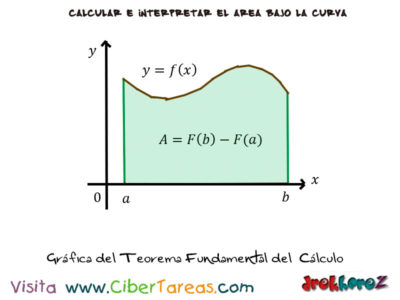
El Teorema Fundamental del Cálculo en Cálculo Integral, en donde tenemos que f(x) es continuar en el intervalo [a,b] y que f(x)+c es la antiderivada de f(x)dx, es decir el área bajo la curva como en la siguiente imagen.

Si recordamos las condiciones iniciales el área A debajo de la curva es cero cuando x=a por lo tanto tenemos que: 0=f(a)+c, donde c=-f(a) para entonces esto cuando x=b recorremos toda el área y esta es A= f(b)-F(a).

Al tener definida la integral, tenemos este análisis nos conduce al teorema siguiente que por cierto es una forma de Teorema fundamental del cálculo .

En el Teorema de Evaluación; si f(x) es continua sobre este intervalo [a,b] entonces donde f(x) es cualquier integral de f(x) es decir F´(x) = f(x)