Aplicación del método de ion-electrón cuando la reacción se desarrolla en disolución ácida en Temas Selectos de Química 2
Para explicar este tema, se va a considerar la siguiente ecuación iónica neta: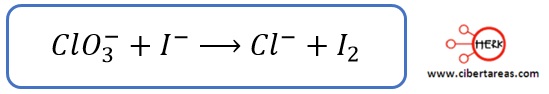
1.-Se escriben dos medias ecuaciones:
-Una para la especie química que se oxida
-Otra para la que se reduce
-Posteriormente se le asignan los coeficientes necesarios para ajustar las cantidades de los átomos principales para este ejemplo, el cloro y el yodo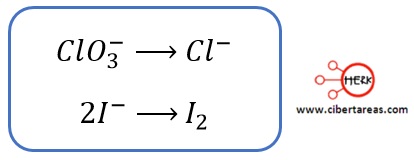
2.-Para equilibrar las átomos de hidrógeno y oxígeno, como la reacción se desarrolla en solución ácida, está permitido agregar H20 e H+ donde sea necesario, y como por cada molécula de agua que se añada en uno de los dos miembros de la ecuación deben agregarse dos H+ en el otro lado
3.-Para siguiente paso, consiste en equilibrar las cargas
-Tenemos que en el lado de los reactivos, para la primera ecuación, se tienen 5 cargas positivas:
-(+6 – 1 = +5)
-Mientras que en el derecho, el de los productos, se tiene solamente una negativa
-La del átomo de cloro
-Entonces se agregan 6 electrones al lado derecho
-Para la segunda ecuación se deben agregar dos electrones del lado de los productos para equilibrar las dos cargas negativas: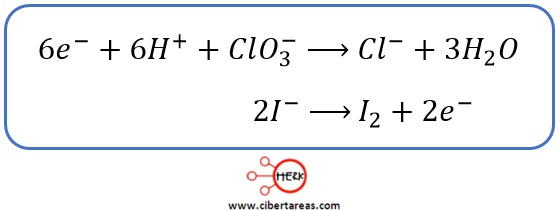
-Tenemos que cuando los electrones aparecen en el lado de los reactivos se trata de una reacción de reducción
-Cuando aparecen en los productos es una reacción de oxidación
4.-En este paso, implica efectuar las operaciones necesarias para igualar los electrones cedidos o ganados
-Se multiplica la segunda ecuación por 3
5.- Se suman ambas semiecuaciones, miembro por miembro, pare tener la ecuación completa y balanceada
-Los electrones, como se encuentran en igual cantidad a ambos lados, se cancelan
-Siempre es necesario que se verifique la igualdad tanto en átomos como en cargas a ambos lados de la ecuación
En el ejemplo anterior se tiene 6H, 6I, 1CI y 3O en cada lado, por lo que se cumple la ley de la conservación de la masa
En lo que se refiere a las cargas, se tiene:
-En el lado de los reactivos:
+6 –6 -I = -1
-En el lado de los productos:
-1 + 0 + 0 = -1
Con lo anterior se concluye que la ecuación está bien balanceada

