El Cálculo de Áreas y Volúmenes en los Modelos Matemáticos en el estudio del calculo y evolución en el Calculo Diferencial, las funciones representan modelos para resolver los problemas de la vida real.

Vamos a analizar distintos ejemplos que te permite entender la importancia:

1.-Un Globo Aerostático asciende desde un punto con velocidad constante de 1.5 m/s a 30 metros del punto de despegue se encuentra una casa. Si [t] es el tiempo en segundos, expresa la distancia que existe entre la casa y el globo en función del tiempo.

Solución:

Utilizando la siguiente formula:

v = d/t entones d = vt

Donde [d] es la distancia, [v] es la velocidad y [t] es el tiempo, Al trascurrir [t] en segundos el globo sube [1.5 t] en metros entonces se aplica el Teorema de Pitágoras para obtener:

2.- La altura de un recipiente cilíndrico es el doble que el radio de su base , expresa el volumen del cilindro en función de su altura.

Solución:

Utilizando el siguiente formula del volumen del cilindro:

V = r²h

Considerando que es el doble del radio de su base, tenemos:

3.- El perímetro de un rectángulo es de 26 unidades expresa el área del rectángulo en función de su largo.

Solución:

Se establecen las dimensiones del rectángulo:

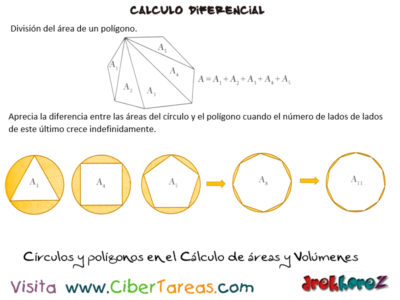
El problema del cálculo de áreas de figuras irregulares o curvas es lo que llevó a los antiguos griegos a utilizar el método del “Agotamiento” hace poco por lo menos 2 500 años. Esta técnico consiste en dividir el área [A] de un polígono en varios triángulos para luego sumar las áreas de los triángulos resultantes.

Claro que esto era mucho más difícil obtener el área de una figura curva. Utilizaba el método de agotamiento que consistía en inscribir y circunscribir polígonos en torno a la figura y a continuación hacer que el número de lados de los polígonos aumentara.

El método en el caso de un circulo con polígonos regulares inscritos.

[A] al área del círculo y [A_n] al área del polígono inscrito con [n] lados. Al aumentar [n] de manera indefinida, parece que [A_n] se aproxima cada vez más al área del círculo. Decimos que el área del circulo es el limite de las áreas de los polígonos inscritos y escribimos en forma simbólica:

Es conveniente aclarar que los griegos no aplicaron explicitamente los limites, pero por medio del método del agotamiento pudieron probar la conocida fórmula del área del circulo

A=𝜋r²