La Definición de Tangente en los Modelos Matemáticos para el estudio del Calculo y su evolución – Calculo Diferencial, vamos a definir el concepto de “Recta Tangente” a una curva dieron como resultado la rama del cálculo que se llama “Calculo Diferencial y el desarrollo se presto 2000 años después del calculo integral.
Gracias a las ideas fundamentales sustentan al Cálculo Diferencias , se lo debemos al Matemático Isaac Newton [1642-1727] y al matemático Alemán Gottfriedd Leibni [1646-1716].
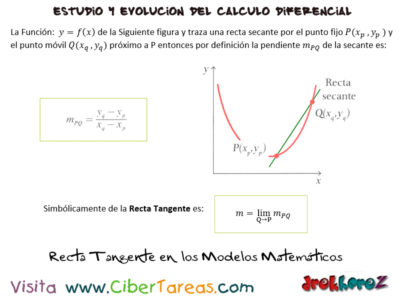
En la siguiente gráfica de la función en donde se aprecia la figura y traza una recta secante por el punto fijo y el punto móvil próximo a P, entonces por definición la pendiente de la secante es:
En el punto Q se mueve a lo largo de la curva de f(x) acercándose a P. En la secuencia de la figura 4 se puede apreciar que la recta secante gira y se aproxima a la recta tangente como su posición limite. La pendiente [mPQ] de la recta secante se acerca cada vez más a la pendiente [m] de la recta tangente simbólicamente esto se escribe así.
En la imagen aprecia “m es el límite de mPQ cuando Q tiende a P”
Las anteriores gráficas se expresa la pendiente m de la recta tangente es el límite de mPQ cuando Q se acerca mucho a P. Por tanto, cuando xq se acerca a XP podríamos usar también la ecuación de la imagen anterior.
