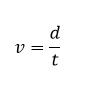Cómo se describe el movimiento rectilíneo uniforme en Física 1

Para ilustrar cómo se describe el movimiento rectilíneo uniforme, analicemos el siguiente ejemplo:

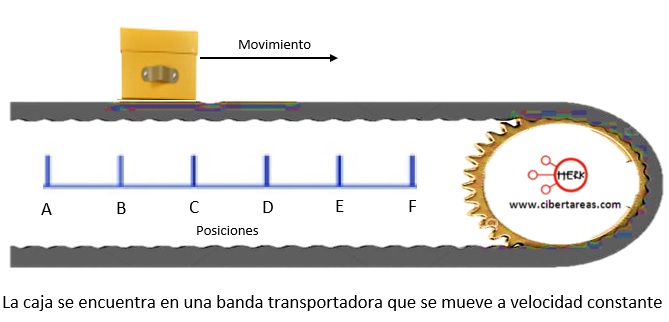
-Es necesario considerar el movimiento de una caja colocada en una banda transportadora que viaja a velocidad constante

Para empezar, se miden las distancias recorridas y los tiempos de recorrido de la botella

Posteriormente se organizan las medidas en una tabla de valores: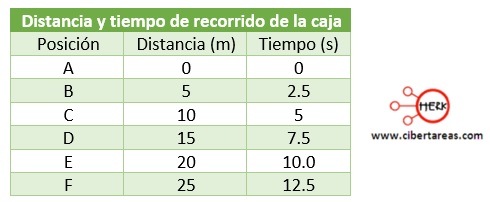

Cabe mencionar que las medidas de las distancias recorridas por la caja y los tiempos que tardó en recorrerlas se tomaron a partir de la posición A, en otras palabras, cuando la botella alcanzó la posición B, la distancia recorrida fue de 5 m y el tiempo transcurrido fue de 2.5 S.

Cuando llegó a la posición C, la distancia recorrida desde A hasta C fue de 10 m y el tiempo de 5 s

Al calcular cuál es la distancia recorrida por la caja a los 10 s, se puede observar la tabla de valores, para este este ejemplo, la caja recorrió́ 20 m

Con esto tenemos que el movimiento rectilíneo uniforme puede describirse mediante una tabla de resultados

En virtud de que la información que proporciona la tabla anterior no permite visualizar con rapidez las características del movimiento rectilíneo de la caja, se puede describir dicho movimiento mediante una gráfica de las mediciones del tiempo y distancias recorridas

Para lo anterior, ubicamos el tiempo en el eje horizontal y la distancia en el eje vertical, como se muestra en la siguiente figura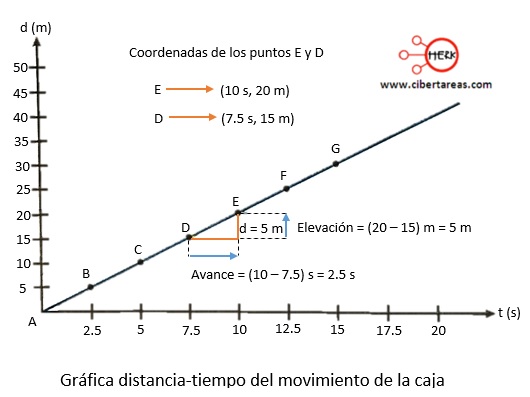

Al graficar los datos de las distancias recorridas de la tabla datos en función del tiempo y unir los puntos, se obtiene una línea recta

De la gráfica anterior se puede obtener la magnitud de la velocidad mediante el cálculo de la inclinación de la línea recta, o sea de su pendiente

La pendiente es:

De esta manera, entre los puntos D y E de la gráfica, la elevación es 20 m – 15 m = 5 m y el avance es 10 S – 7.5 s = 2.5 S

Para determinar la pendiente usamos estos dos puntos: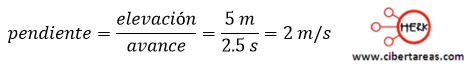

Esto quiere decir que la magnitud de la velocidad de la caja es de 2 m/s

Como la gráfica es una recta, la pendiente es la misma a lo largo de ella, si se compara la magnitud de la velocidad de la caja con la pendiente, se puede concluir que la pendiente de la gráfica distancia-tiempo corresponde a la magnitud de la velocidad

Con esto tenemos que entre más inclinada se la pendiente de una gráfica distancia tiempo, mayor es la rapidez

En la siguiente gráfica se muestra la distancia-tiempo de dos aviones, uno viaja a 100 m/s y el otro a 200 m/s, la pendiente de la recta que representa al avión más rápido está más inclina que la pendiente de la recta que representa al avión más lento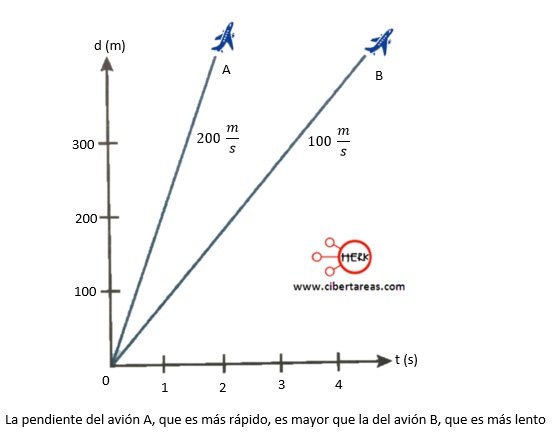

Al calcular la magnitud de la velocidad (rapidez) para la caja, para cada par de posiciones obtendremos los valore que se muestran en la siguiente tabla: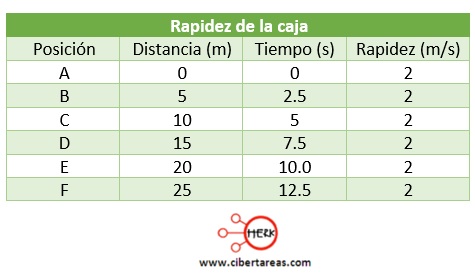

Al trazar una gráfica de la magnitud de la velocidad (rapidez)-tiempo, se obtiene una recta paralela al eje horizontal, esto lo podemos observar en la siguiente imagen: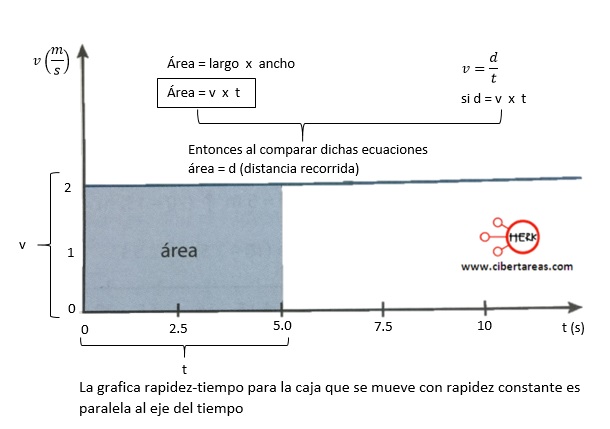

Esto se debe a que, en todo instante, la rapidez o magnitud de la velocidad se mantiene constante

La gráfica rapidez-tiempo es útil porque el área entre la curva y el eje del tiempo representa la distancia recorrida por la caja (o cualquier otro móvil)

Analizando el grafico anterior, tenemos que el área sombreada, es la distancia recorrida por el móvil a los 5 s, y corresponde a la de un rectángulo, y el área de un rectángulo se obtiene de multiplicar largo por ancho, en nuestro caso, el área es 2 m/s X 5 s, cuyo resultado es igual a la distancia recorrida de 10 m

El área sombreada bajo la línea horizontal de la gráfica representa la distancia recorrida para un tiempo de 5 s

Podemos concluir que las gráficas distancia-tiempo y rapidez-tiempo son otra alternativa para describir el movimiento rectilíneo uniforme

Se puede describir el movimiento de la caja sobre la banda transportadora mediante una ecuación (fórmula), ésta se obtiene de la ecuación de la pendiente de la gráfica distancia-tiempo, es decir: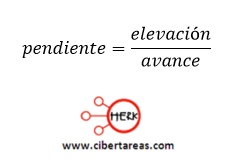

De la siguiente grafica podemos concluir que:

1 Elevación = d

2 Avance = t

3 Pendiente = v

Por lo tanto:

Esta ecuación se característica del movimiento rectilíneo uniforme cuando la velocidad es constante

Para el ejemplo de la caja sobre la banda transportadora, como la velocidad es constante e igual a v = 2 m/s la ecuación que representa dicho movimiento es:

d = (2 M/s)t

En esta ecuación, d se mide en metros y t en segundos

Con esta ecuación se pude describir el movimiento de la caja, ya que es posible calcular la distancia recorrida para cualquier instante

Tenemos que para t = 5 s, la distancia recorrida es:

d = (2 M/s)t (5s) = 10 m

Este valor coincide con el obtenido en la gráfica rapidez-tiempo para t = 5 s