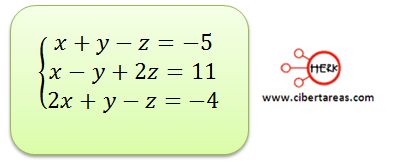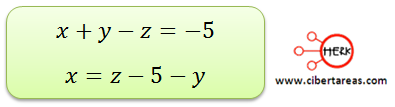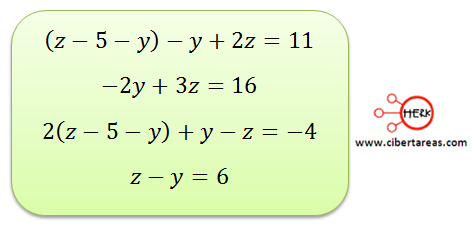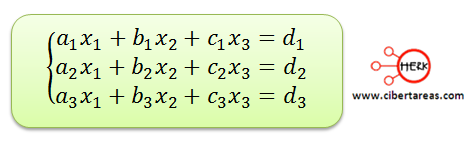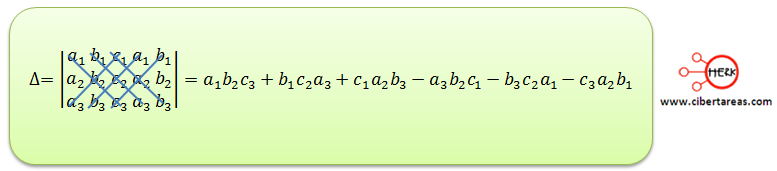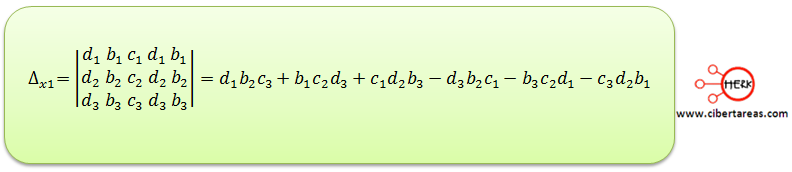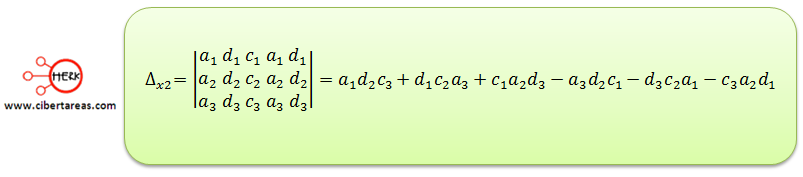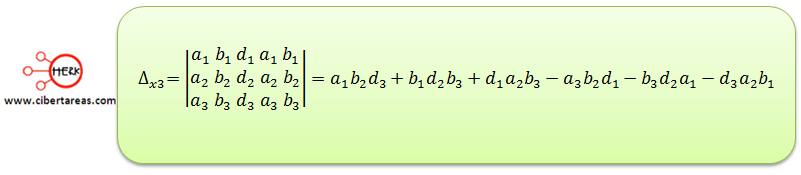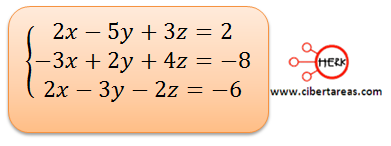Ecuaciones simultaneas de tres por tres con solución o sin solución – Matemáticas 1

Partiendo del método de sustitución, se puede simplificar un sistema de tres ecuaciones y convertirlo en un sistema de (2 x 2). Tenemos el siguiente ejemplo de este sistema:

Para poder resolver este sistema, primero debemos de elegir la ecuación y la variable más sencillas y posteriormente despejamos la incógnita “x”.

Ahora sustituimos el valor de “x” en las otras dos ecuaciones

Estas ecuaciones forman un sistema de (2 x 2) que se puede resolver por cualquiera de los métodos.

Hagámonos la siguiente pregunta:

¿Es posible hallar los valores de las variables que satisfagan el sistema?

Cuando el sistema es:

Para esto emplearemos un método conocido como determinantes para resolver este sistema. Un determinante es un arreglo de números que, generalmente se desprende de un sistema de ecuaciones que se quiere resolver. Este sistema permite definir varios determinantes, el del sistema Δ y los de cada una de las incógnitas:

El determinante del sistema está constituido por los coeficientes asociados a cada incógnita, mientras que para los determinantes de cada incógnita se necesita sustituir los coeficientes del determinante del sistema por los términos constantes, es decir:

 Vamos a ver como se realiza el cálculo de estos determinantes, primero debemos encontrar el valor del determinante del sistema (Δ), dado el determinante, le podemos agregar valores de las dos primeras columnas en la cuarte y quinta columna del determinante. En total contaremos con cinco columnas, siempre tenemos que hacer la multiplicación diagonalmente.

Los productos van a adquirir un valor negativo si van de la zona inferior izquierda a la zona superior derecha, y si se dirigen de la zona superior izquierda a la zona superior derecha serán positivos.

Para encontrar Δx₁ se debe de sustituir la primera y la cuarta columna por las variables d₁, d₂, d₃

Para encontrar Δx₂ se debe de sustituir la segunda y la quinta columna por las variables d₁, d₂, d₃ 

Para encontrar Δx₃ debemos sustituir la tercera columna por las variables d₁, d₂, d₃

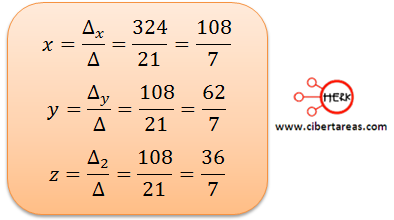
Para finalizar, la solución al sistema está dada por las siguientes relaciones:

Vamos a ver el siguiente ejemplo, en el cual vamos a determinar el siguiente sistema de ecuaciones, con las variables x₁, x₂, y x₃ las cuales adquieren la forma x, y, z.

Hagamos el arreglo de los coeficientes para determinar los valores Δ, Δ_x, Δ_y, Δ_z, tenemos como primer paso en definir Δ

Ahora vamos a calcular Δx

Ahora calculemos el discriminante Δy

Por ultimo vamos a obtener Δz

Con esto obtenemos las definiciones necesarias para conocer los valores de x, y, z.