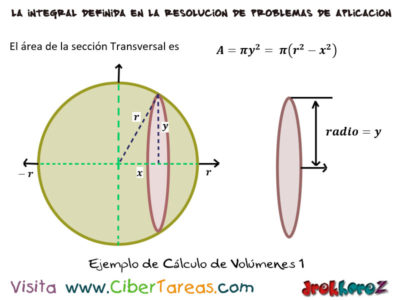
Ejemplos de Cálculo de Volúmenes en Cálculo Integral logramos demostrar el volumen de una esfera de radio [r].La solución es al situar la esfera con su centro en el origen de manera que las secciones sean perpendiculares al eje x.

Ya que el radio y de una rebanada cualquiera es de acuerdo con el teorema de Pitágoras. Por lo tanto el área de la sección transversal es:

Entonces por la definición de volumen tenemos que:

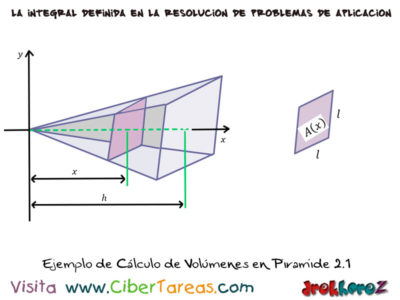
En el siguiente ejemplo vamos a encontrar el volumen de una pirámide cuya base es un cuadrado de lado [L] y altura [H], en controversia colocamos el vértice de la pirámide en el origen y el eje [x] lo hacemos coincidir con su eje central designaremos, la sección transversal con una cuadrado de lado [l] y la Altura [H].

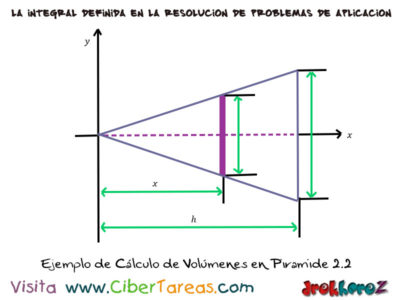
Ya que la solución por conveniencia, colocamos el vértice de la pirámide en el origen y el eje [x] lo hacemos coincidir con su eje central, designaremos la sección transversal con un cuadrado de lado [l] lo podemos poner en función de [x] considerado los triángulos semejantes de la siguiente figura:

El área de la sección transversal, ya que la pirámide se encuentra entre x=0 y x=h por lo tanto en su volumen: