El Calculo de Volúmenes en Cálculo Integral, en secciones paralelas en elementos de secciones, de la misma forma que se realiza con el área de regiones planas, aquí se utilizara las Integrales Definidas para encontrar los volúmenes de ciertos sólidos en tercera dimensión.
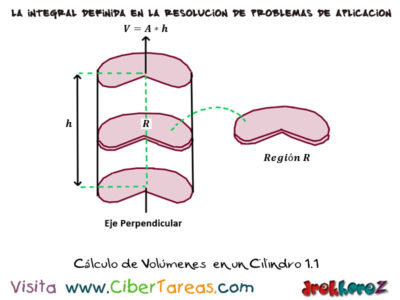
Un cilindro cualquiera con Sección Transversal [R] es un sólido formado por las traslación de la región [R] a largo de un “Eje Perpendicular” a ésta. Si [A] es el área de la región [R] y ésta se traslada a lo largo de una distancia [h] entonces el volumen generado por la sección es V= Axh como se muestra en la siguiente imagen:
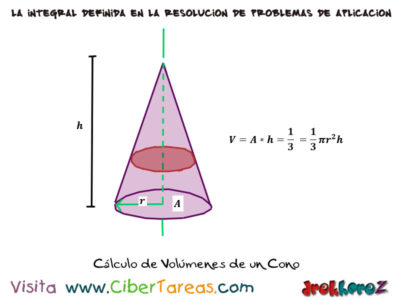
Apreciadamente figuras de algunos sólidos de volúmenes muy familiares, éstos son:
Un cilindro recto de radio [r] y altura [h] una caja rectangular de longitud [l], ancho [w] y altura [h] un cono de radio[r] y altura [h].
Si imaginamos que un solido de forma de rebanada, se encuentra situado entre [x=a y x=b].Al tomar una área arbitraria en dicha rebanada como A(x), en perpendicular al eje X y que varia continuamente a lo largo del eje. Entonces podemos decir que si se suman los volúmenes de todas estas rebanadas, se obtiene una aproximación para el volumen total del sólido aquí se puede apreciar:
En dicha aproximación va a mejorar cuando n->∞ es decir las rebanadas se van adelgazando, entonces estamos utilizando de nueva cuanta en las “Sumas de Riemann” pero considerando volúmenes con lo que tenemos definición:
Un Volumen de un solido, sea que se encuentre en [x=a] y [x=b] si el área A(x) de la sección transversal del solido esta en un plano perpendicular al eje [x] u varía continuamente a través de este, entonces el volumen del solido es:
Cuando usemos la fórmula del volumen que es importante recordar que A(x) es una sección variable dependiendo de la forma del sólido, obtenida al efectuarse.