Ejemplos de las Derivadas de Funciones Implícitas en Cálculo Diferencial, encuentra la derivada de x² + y² = 25. Ya que al derivar término a términos tenemos que:

d/dx x² + d/dx y² = d/dx(25)

2x + 2y dy/dx = 0

2y dy/dx = 0

2y dy/dx = – 2x

dy/dx = – 2x/dy = – x/y

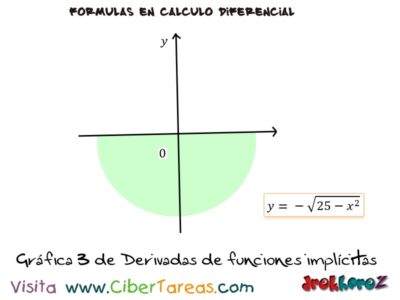
En la comprobación al hacer la función tenemos:

y= √25-x2

dy/dx = 1/2 (25-x2) -1/2 (-2x) = – x/(25-x2) 1/2 = – x/ √25-x²

Pero si en el denominador sustituimos √25-x2 por y obtenemos el mismo resultado que en el ejemplo 1:

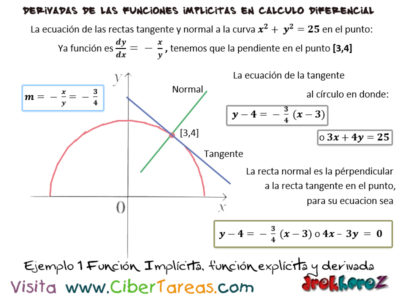
dy/dx = – x/y tenemos que la pendiente en el punto [3,4] es:

m= – x/y = -3/4

En la ecuación de la tangente al círculo en [3,4] es:

y-4 = – 3/4(x-3) o 3x+4y=25

Para la recta es la perpendicular a la recta tangente en el punto luego su ecuación es:

y-4= – 3/4(x-3) o 4x-3y=0

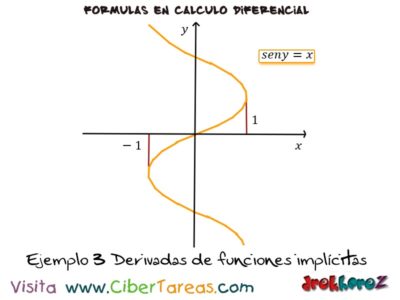
Para calcular dy/dx de la ecuación sen y = x:

Tenemos que d/dx sen y = dx/dx
cos y dy/dx = 1
dy/dx = 1 /cos y