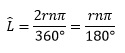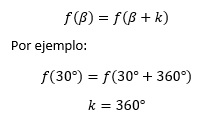Gráfica de la función seno en Matemáticas 2
Para poder graficar la función seno, es importante seguir los siguientes pasos en los cuales se irá elaborando la gráfica de dicha función![]()
Material necesario:
-Papel milimétrico
-Transportador
-Calculadora o tablas trigonométricas
1.- En el papel milimétrico se traza una circunferencia de radio r (es necesario determinar un valor adecuado), se divide esta circunferencia en los ángulos que apareen en la siguiente figura: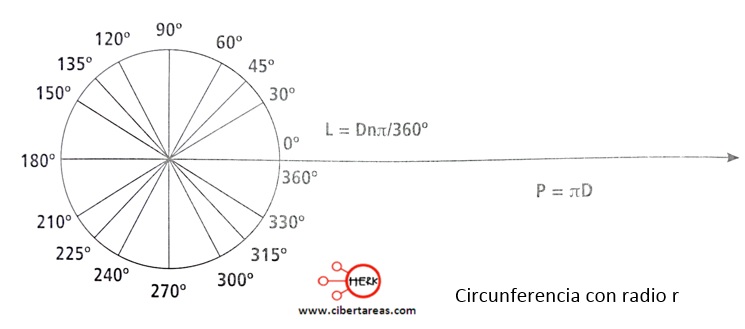
2.- Se traza un sistema de eje coordenados, se establece el origen exactamente en 0°, el eje de las abscisas (eje x) debe tener en el trazo una longitud igual al perímetro de la circunferencia de radio r (es importante considerar el valor de r que se eligió)
3.- Se calcula la longitud de arco de la circunferencia para 30°, esta longitud se obtiene con la fórmula:
Una expresión equivalente es:
Con base en el radio que se asignó, es necesario encontrar la longitud asociada a 30°
Se traslada al eje de las x
Se realiza el mismo proceso para transferir cada arco en circunferencia
Con esto se encuentra el equivalente de grados en radianes (números reales), de acuerdo con le radio que se asigno
4.- Se encuentra el valor de la función seno para cada ángulo
Como referencia tenemos los siguientes valores: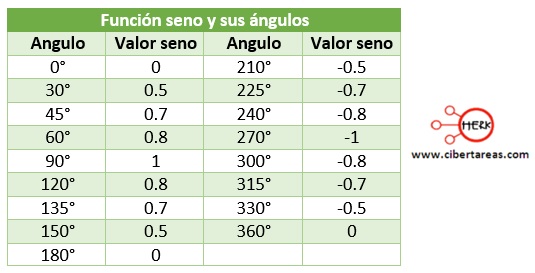
5.-con la tabla anterior es necesario conformar parejas ordenadas y localizar los respectivos puntos, tal y como se muestra en la siguiente imagen: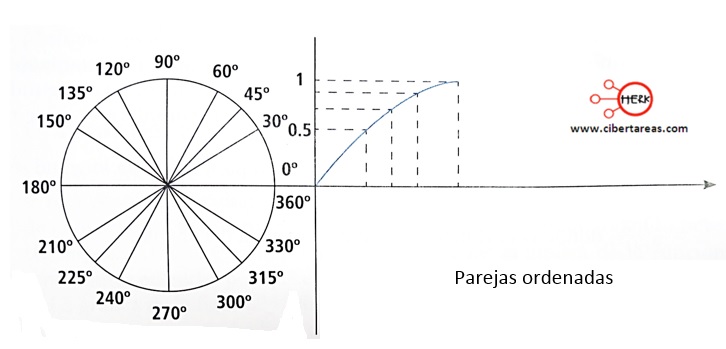
Se establecen parejas entre domino y contradominio para la función seno, como se muestra en la siguiente figura: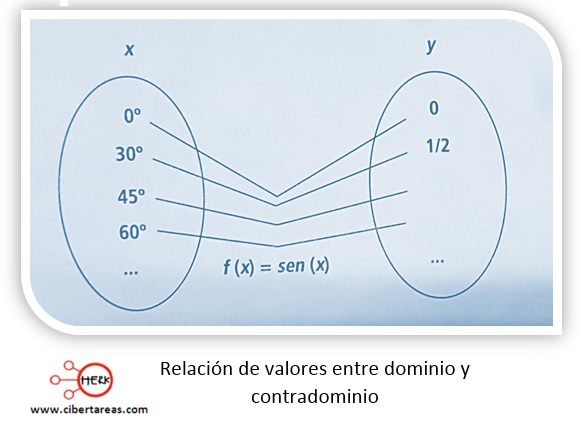
6.- Al observar el avance de la función seno tenemos: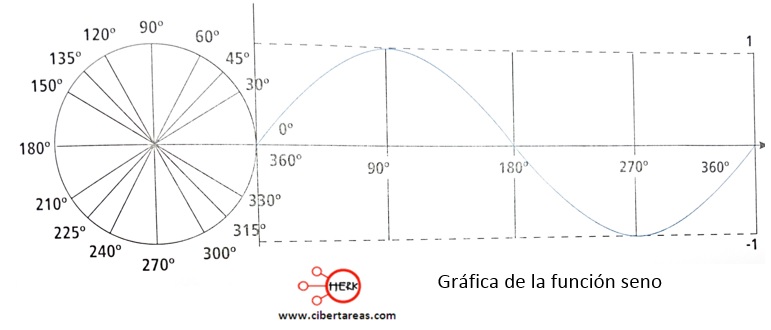
A partir de la gráfica de la función seno se define:
-La función toma valores en su contradominio de -1 a 1
-Es una función acotada, en otras palabras, tiene fronteras y no pasa más allá de determinados valores
-La función crece para valores angulares en el primer y en el cuarto cuadrante, en el segundo y en el tercer cuadrante la función decrece
-La función es positiva en el primer y segundo cuadrante, y negativa en el tercer y cuarto cuadrante
-La función es periódica, es decir:
Por ejemplo:
-La función corta el eje de las x en 180°, 360°, 540°,…, es decir, en (n)(180°), con n como numero natural