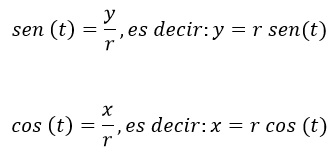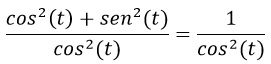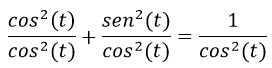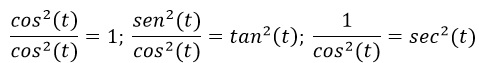Identidades pitagóricas en Matemáticas 2
Como se sabe, la forma convencional de representar un punto en el plano cartesiano es por medio de una pareja de números (x, y)
En la siguiente figura, tenemos la representación de un móvil que describe un trayectoria circular de radio r, dada esta condición, el móvil se localizaba en un primero momento en (r, 0), si el móvil continua su movimiento y llega al punto (x, y) de la circunferencia, entonces se puede representar su posición con respecto a su ángulo (para este caso 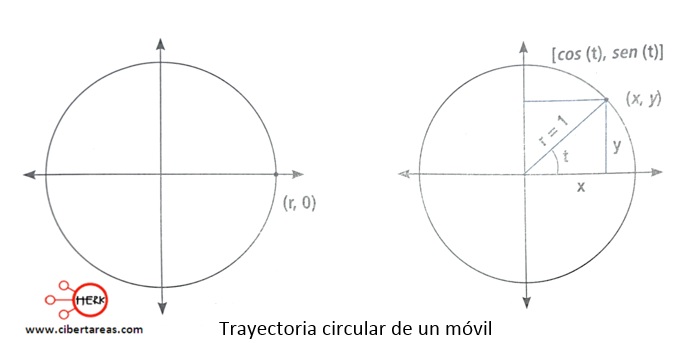
Es importante mencionar que para mantener el equilibro de una ecuación de igualdades debe existir valores equivalentes en cada uno de sus lados
Las funciones se describen como:
La coordenada (x, y) se puede representar ahora de esta forma:
![]() puede tomar valores de 0° a 360°
puede tomar valores de 0° a 360°
Si el círculo es de radio uno (r = 1), entonces las coordenadas (x, y) son:
![]() , es decir: [cos (t), sen (t)]
, es decir: [cos (t), sen (t)]
Analíticamente las expresiones: ![]() , o bien su equivalente: x2 + y2 = 1, determinan geométricamente un circulo de radio uno
, o bien su equivalente: x2 + y2 = 1, determinan geométricamente un circulo de radio uno
Al observar la expresión: ![]() nos damos cuenta que es una igualdad, en trigonometría a estas igualdades se conocen como identidades trigonométricas, y cuando se refiera a la igualdad del teorema de Pitágoras: x2 + y2 = 12, se habla de identidad pitagórica
nos damos cuenta que es una igualdad, en trigonometría a estas igualdades se conocen como identidades trigonométricas, y cuando se refiera a la igualdad del teorema de Pitágoras: x2 + y2 = 12, se habla de identidad pitagórica
Relaciones que se dan en la siguiente identidad pitagórica:
Si se dividen ambos términos por cos2 (t) no se latera la igualdad:
Al distribuir cos2 (t) en ambo sumados del primer término:
Es importarte observar que:
Con lo anterior de obtiene una nueva identidad pitagórica: