El Método de Discos y Ejemplos en Cálculo Integral, cuando se hace girar la región de área que está debajo de una función alrededor del Eje X o algún otro eje, lo que se obtiene es un “Solido de Revolución“.El volumen de este sólido se obtiene con la integral como en la siguiente imagen se muestra:
Esto siempre que se gira una superficie invariable, elementos de sección pequeños cilindros de área.
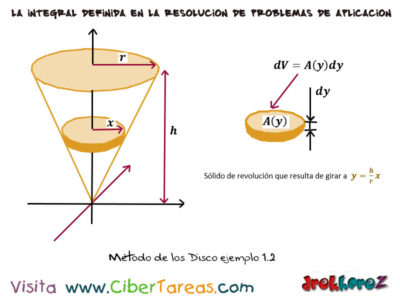
Ejemplo 1 en el Volumen del Cono Circular, para demostrar que el volumen de un cono cuyo radio de la base es [r] y de altura [h] viene dado por:
En este cono se genera al girar una recta de pendiente m=h/r alrededor del eje y.Ya que el solido que resulta de girar la región formada por la recta y=h/r x, el eje y la recta y=h es el que se muestra en la siguiente imagen, evidente que las revenadas o discos son perpendiculares al eje de que modo que si:
Entonces el volumen es:
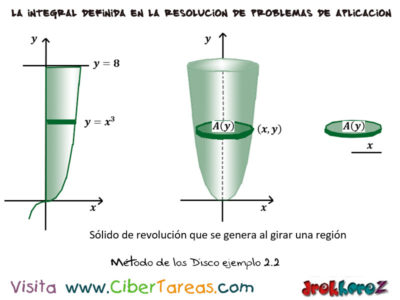
Ejemplo 2 del Centro de Masa en Calculo Integral, Vamos por el siguiente ejemplos para encontrar el volumen del sólido que se obtiene al hacer girar la región limitada por y=x3, y=8 y y=0 alrededor del eje y.
Ya que el solido que resulta al girar la región de la función es el que se muestra en la siguiente imagen, a que evidente las rebanadas a discos que son perpendiculares al eje y de tal modo que si en la imagen que se muestra aquí:
y = x3 entonces x=y1/3 en este caso x es el radio.
Por lo tanto el volumen del sólido que se genera es: