Semejanza en los triángulos en Matemáticas 2

Cuando se analizan las figuras geométricas y se reconoce alguna igualdad entre sus formas, a esto se le llama semejanza, el tamaño de las figuras puede ser distinto, por ejemplo:

-Un cuadrado de 1 centímetro de lado es semejante a un cuadrado de 1 kilómetro de lado, ya que ambas formas tienen las mismas propiedades:

-Cuatro lados iguales entre si

-Cuatro ángulos rectos y lados paralelos entre si

Para el caso de los triángulos ocurre lo mismo, para saber que dos triángulos son semejantes solo es necesario comprobar que se cumple alguna de las condiciones siguientes llamada, criterios de semejanza de triángulos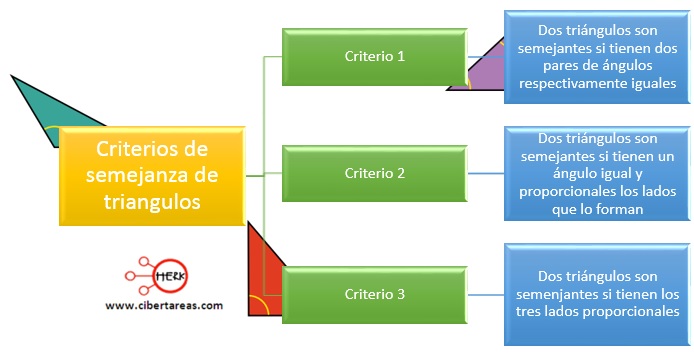

Criterio 1

Dos triángulos son semejantes si tienen dos pares de ángulos respectivamente iguales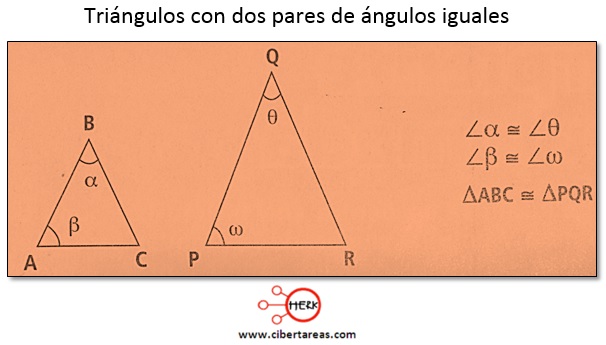

Criterio 2

-Dos triángulos son semejantes si tienen un ángulo igual y proporcionales los lados que lo forman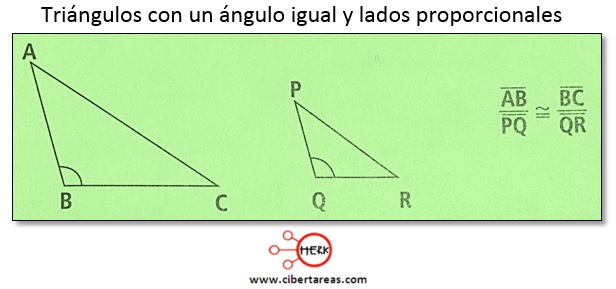

Tal es el caso de dos triángulos con un ángulo de la misma magnitud:

Al comparar la longitud de

Para este caso en particular, al comparar

Uno de los métodos para comprobar que existe una relación de proporcionalidad es:

-Multiplicar los extremos y los medios de la proporción

-Si son iguales los productos, entonces la relación de proporcionalidad es correcta

En el ejemplo del asistente matemático se alcanza la validez de la proporción:

6 ∙ 4 = 24 y 3 ∙ 8 = 24

Criterio 3

-Dos triángulos son semejantes si tienen los tres lados proporcionales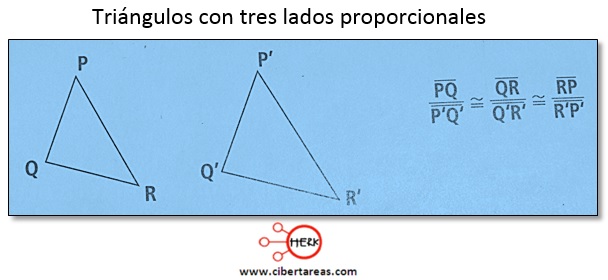

Cuando dos triángulos están construidos de manera que los lados guardan una relación de proporcionalidad, se puede asegurar que los triángulos son semejantes