Sumando a la Riemann – Cálculo Integral. Al considerar n rectángulos de ancho iguales Δx y alturas f(x) y se toman estas como la ordenada correspondiente al valor de un punto de la curva en donde [x] es la abscisa del punto medio del subintervalo Δx entonces el área del rectángulo de aproximación en ese punto es f(x)Δx. En el área A limitada en su parte superior por la gráfica de una función continua y positiva, en su parte inferior por el eje x, a la izquierda por la recta x= a y a la derecha por la recta x=b se puede aproximar a la suma de las áreas de esos rectángulos.
Donde Δx se puede determinarΔx = b-a/n y n es el número de franjas que deseamos:
En la expresión anterior se llama Suma de Riemann en honor al matemática en honor al Matemático Alemán Bernhar Riemann quien creó la definición de integral que utilizamos en la actualidad.
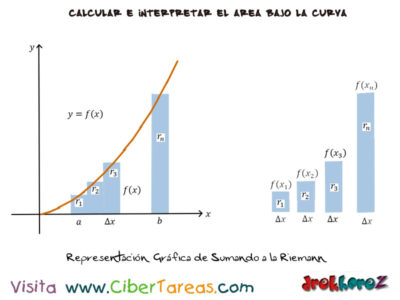
La representación gráfica de Sumando a la Riemann:
Cuando el número de rectángulos n tiende a infinito, el cálculo de A de aproxima con al exactitud a su valor real que en la actualidad ello esta fiera toda la discusión. Definimos el área de la región mencionada de la siguiente manera: