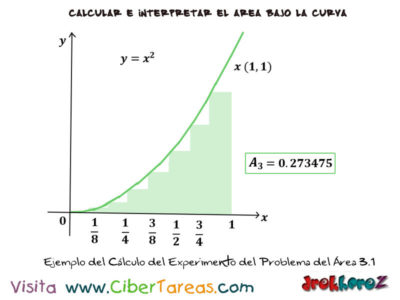
Ejemplos del Problema del Área en Cálculo Integral, al considerar una de las figuras que sugieren a continuación al intentar estimar el área [A] debajo de la parábola y=x desde x=0 hasta x=1 suma las áreas de los rectángulos dibujados.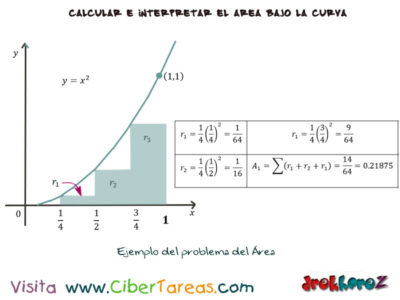

Vamos analizar el ejemplo de la primera figura:

En el calculo del experimento queda de la siguientes imágenes:

Siendo evidente el área debajo de la curva es mayor que A₁ y menor que A₂ es decir:

0.21875 < A < 0.46875

Al aumentar el número de franjas obtenemos mejores estimaciones, tanto con los rectángulos por debajo de la curva como con los que se ubican por encima de ellos como en la siguiente imagen:

0.273475 < A < 0.3984375

Al usar 50 franjas el área se encuentra entre 0.3234 y 0.3434 con mil franjas se encuentran entre los 0.33283 y 0.33383 logrando promediar estos números se obtienen que A= 0.33333.

Demostrando que a medida que el número de franjas [n] crece indefinidamente, las sumas inferiores y superiores que tienden a 1/3 como limite es decir en el limite de la anterior imagen.