Tiro horizontal en Física 1

Debemos considerar que el movimiento de una pelota lanzada horizontalmente desde una altura h y con una velocidad inicial

 y el de un paquete con víveres que se deja caer desde un avión en pleno vuelo son ejemplo de este tipo d movimiento

La trayectoria que describen estos objetos es una curva llamada parábola, por esta razón tales movimientos se conocen como movimientos parabólicos, tenemos como ejemplo:

En estas condiciones, la pelota y el paquete con vivieres reciben el nombre de proyectiles, por proyectil entendemos a cualquier cuerpo u objeto que arrojado mediante un impulso continua en movimiento en virtud de su inercia y de la aceleración de la gravedad

Debemos considerar que, en este movimiento, la aceleración es constante y perpendicular a la dirección de la velocidad inicial

Para el caso de objetos que se arrojan cerca de la superficie terrestre, la aceleración a la que están sometidos es la aceleración de la gravedad

Para describir el movimiento de un objeto en un tiro horizontal, se necesita conocer:

-Posición

-Velocidad

-Aceleración

Lo anterior en todo momento a lo largo de la trayectoria

Para esto:

-Se tiene que asociar un sistema de coordenadas cartesianas, de manera que su origen coincida con la posición inicial del objeto cuando se arroja horizontalmente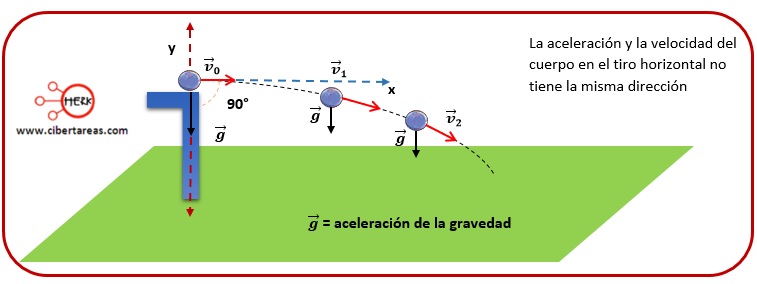

Tenemos que una vez que el sistema de coordenadas cartesianas se ha asociado, es importante considerar que dos observadores describen e informan lo que ven desde distintas posiciones muy “alejadas” del movimiento, para esto tenemos: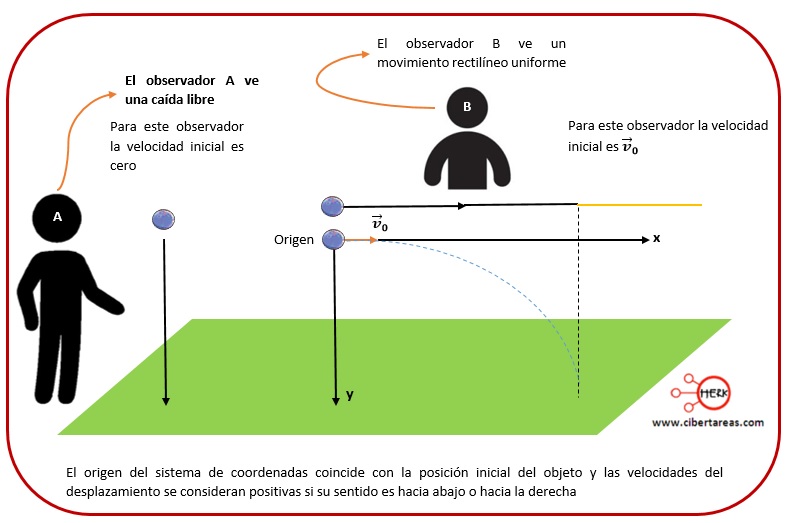

Analizando el diagrama anterior, tenemos que:

-El observador A:

-Ve que la trayectoria de dicho objeto es una línea recta vertical, ya que para él el objeto se encuentra en caída libre, es decir, el movimiento del objeto visto por el observador A es un movimiento rectilíneo uniformemente acelerado con velocidad inicial vertical igual a cero

-Este observador no se da cuenta de que el objeto avanza horizontalmente, ante esto, empleará las ecuaciones del movimiento rectilíneo uniformemente acelerado (cada libre) para describir el movimiento.

-El observador B:

-Se encuentra a una gran altura respecto del objeto en movimiento

-Cree que dicho objeto se mueve a lo largo de una trayectoria horizontal a velocidad constante

-Este observador no se percata de que el objeto además de avanzar horizontalmente, desciende

-Con o anterior, el observador B emplea las ecuaciones del movimiento rectilíneo uniforme para describir el movimiento del objeto.

A manera de conclusión tenemos que bajo estas condiciones, el observador A describe el movimiento del objeto a lo largo del eje y, mientras que el observador B lo hace a lo largo del eje x, de acuerdo con el sistema de coordenadas cartesianas empleado

De esta manera, la distancia recorrida por el objeto según A se denota por y, y la distancia recorrida B se denota por x

La comunicación entre los observadores permite conocer con precisión la posición real del objeto, es decir, sus coordenadas en el plano cartesiano:

En donde:

Para poder conocer la distancia que hay entre el objeto y el origen del sistema de coordenadas (magnitud del vector de posición) desde nuestra posición, tomando en cuenta las coordenadas x y y, se utiliza la siguiente ecuación:

En donde r es la magnitud del vector de posición que va del origen a la posición del objeto, como se muestra en la siguiente figura: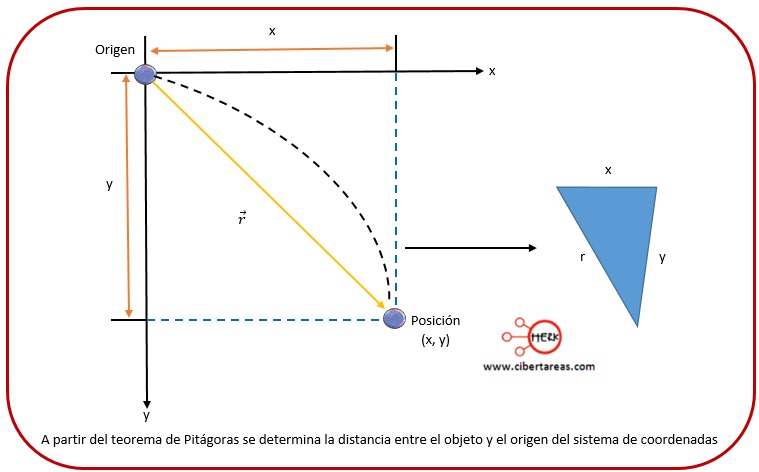

Tenemos que la velocidad medida por el observador B se denotará por v_x y las velocidades inicial y final, para cualquier instante, vistas por A, se denotara por v_0y y v_y, respectivamente

De acuerdo con esta convención, la velocidad del objeto para cada observador es:

En donde:

Para un observador que ocupa una posición igual a la nuestra al momento de leer este texto, la magnitud de la velocidad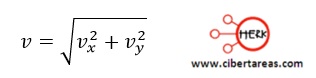

En donde v es la magnitud de la velocidad

La dirección de la velocidad

En donde θ es el ángulo entre

Tenemos que la descripción del movimiento del objeto se completa cuando se proporciona la aceleración del objeto en cada instante

En otras palabras, un objeto arrojado horizontalmente a cierta altura de la superficie terrestre está sometido a la aceleración de la gravedad

Es necesario destacar que si se toman dos esferas iguales mantenidas al mismo nivel y una de ellas se deja caer mientras la otra se lanza horizontalmente, las dos llegarán al piso al mismo tiempo, como se muestra a continuación: