Transformación de unidades en Física 1
Actualmente se pueden utilizar diversas unidades para medir la misma magnitud, de igual manera para medir el tiempo que vive una persona se emplean años, mientras que para medir el tiempo que dura un partido de fútbol se utilizan minutos
De esta manera, al utilizar diversas unidades para distintas actividades y trabajos es necesario convertir la cantidad expresada en una unidad determinada a otra unidad
En la conversión de unidades se presentan dos tipos generales de problemas: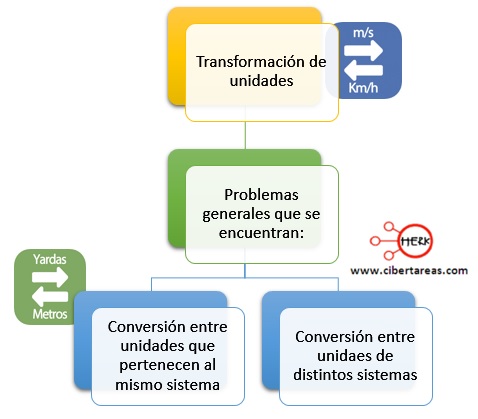
Conversión entre unidades que pertenecen al mismo sistema
-En este caso, la conversión se realiza de una unidad mayor a otra menor, o viceversa
-Ejemplo:
-De centímetro (cm) a kilómetro (km)
-De segundo (s) a microsegundo (µs)
Conversión entre unidades de distintos sistemas
-Ejemplo:
-Convertir libras (lb) del Sistema Inglés a kilogramos (kg) del SI
Para los casos anteriores, es suficiente ejecutar una operación aritmética; basta con multiplicar la cantidad que se desea cambiar por un factor de conversión
Para saber que es un factor de conversión, analicemos lo siguiente:
Razonamientos algebraicos
-Razonamiento 1
-Las unidades se pueden manejar algebraicamente igual que los números
-Esto es, se suman, restan, multiplican y dividen de la siguiente manera:
-Razonamiento 2
-Con excepción del cero, cualquier número dividido entre sí mismo da uno (1)
-De igual manera, cualquier unidad dividida entre sí misma da uno (1)
-Razonamiento 3
-Con base en lo anterior, cualquier unidad dividida entre su equivalencia también da uno (1)
-A la razón algebraica que resulta se le da el nombre de factor de conversión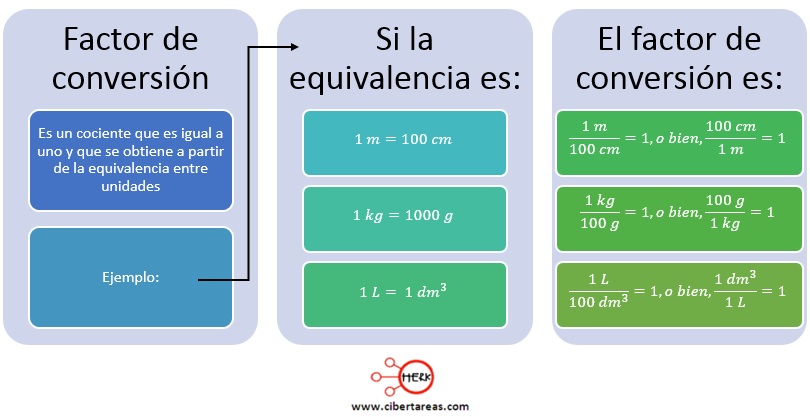
-Para obtener el factor de conversión se debe conocer la equivalencia entre unidades
-Razonamiento 4
-Cualquier número multiplicado por uno (1) da el mismo número; esto es, el número original no se altera en su magnitud
-De igual manera, cualquier medida multiplicada por uno (1) da la misma medida, es decir, la medida original no se altera, por ejemplo:
-A partir de este razonamiento es fácil comprender que es válido multiplicar cualquier medida por un factor de conversión, sin que por ello afecte su magnitud
Es importante recordar que todo factor de conversión siempre es igual a uno (1), con esto se puede afirmar que cualquier problema de conversión de unidades puede reducirse a multiplicar la cantidad por el factor de conversión apropiado
Ejemplo 1:
-¿A cuántos kilómetros corresponden 4728 m?
Solución:
-Lo que se pide es convertir la unidad de metros a kilómetros
-Como punto número uno:
-Se tiene que buscar el factor de conversión adecuado a partir de la equivalencia
-Dicho factor de conversión deberá tener en el dividendo la unidad m y en dividendo la unidad km
-Considerando que la equivalencia es 1 km = 1000 m, entonces el factor de conversión deberá ser: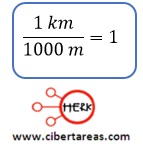
-Como paso numero dos:
-Se multiplica la cantidad original por el factor que se acaba de establecer: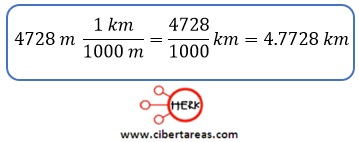
-El factor se escogió de manera que la unidad del metro se eliminara, por lo tanto el resultado es: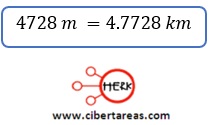
Ejemplo 2
-Observa las siguientes equivalencias:
-Cuando no se sabe la equivalencia directa entre una unidad y otra, como es el caso de este ejemplo, se pueden utilizar relaciones intermedias



