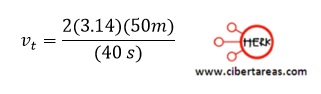Velocidad lineal (tangencial) en Física 1
Analicemos la imagen siguiente: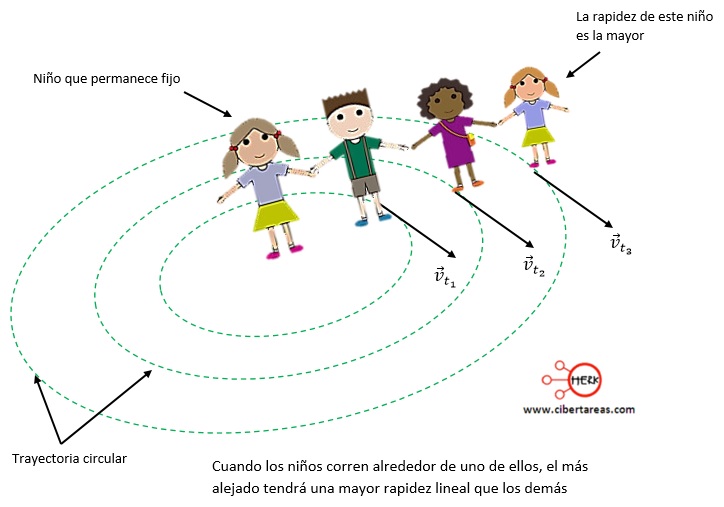
La imagen anterior muestra que, si cuatro niños se toman de la mano, y uno de ellos se queda fijo como pivote, cuando los demás empiezan a correr a su alrededor, el niño más alejado se tiene que soltar para evitar caerse, esta acción de soltarse tiene una justificación: no puede mantener su rapidez, la cual es mayor que la de los demás niños
Lo anterior se debe a que el niño más alejado recorre una distancia diferente (el perímetro del circulo que describen en su movimiento en cada vuelta), este niño al correr un mayor perímetro que los demás en el mismo intervalo de tiempo, tiene mayor rapidez
Para justificar este razonamiento, se tiene que parir de la definición de rapidez, la cual establece que: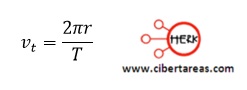
En donde:
r = radio del circulo
t = periodo
vt = magnitud de la velocidad lineal o tangencial
De esta ecuación, a manera de conclusión tenemos:
-Conforme aumenta el radio de la trayectoria circula (r), la magnitud de la velocidad lineal también aumenta
Si no se conoce el periodo de un movimiento circular uniforme, pero si su frecuencia, entonces la magnitud de la velocidad lineal (rapidez lineal) se puede calcular por:
Ejemplo del cálculo de la velocidad lineal (tangencial), problema:
-Calcula la rapidez lineal de un atleta que corre de manera uniforme alrededor de una pista que tiene una trayectoria circular de radio igual a 50 m
-El tiempo que emplea en dar una vuelta completa es de 40 s
-Solución
-Datos
r = 50 m
T = 40 s
vt = ?
-Sustitución