Ángulos en el plano en Matemáticas 2
Al pasar el tiempo, la humanidad fue identificando como su ingenio podía ser aplicado en el entorno para gozar una mejor calidad de vida, como ejemplo de esto tenemos el desarrollo geométrico, el cual ha brindado aportes importantes y aplicables tanto a la ingeniería como a la medicina
En algunos momentos, las técnicas de medición fueron indispensables y trascendentales para poder resolver el problema de como unir dos poblados que estaban separados por un accidente geográfico, como:
-Rio
-Cañones
-Arroyos, etc.
Con esto, surgió la idea de crear un puente para unir ambas zonas
Por ejemplo:
-Puente Brest, en Francia
-Este puente giratorio, están constituido por un pilar circular que puede girar 90°
-Fue unos de los primeros construidos hace más de un siglo sobre el rio Penfeld
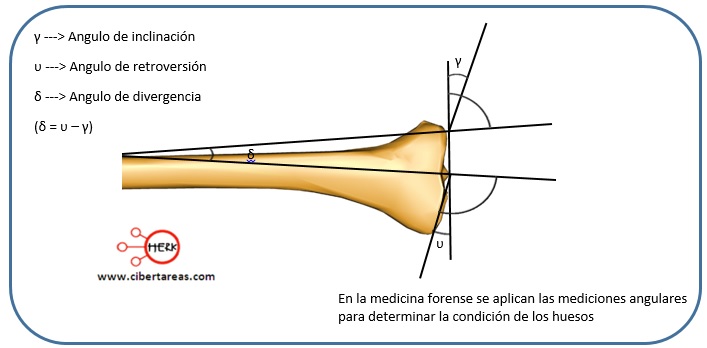
Otra aplicación de las técnicas para medir ángulos es en la medicina, esto se da en los estudios anatómicos, por ejemplo:
-Análisis de la tibia
-Se determinan los ángulos de retroversión e inclinación
-Para esto se emplea:
-Paralelógrafo
-Papel milimetrado
-Para llevar a cabo esto, es importante tener una lata capacidad visual para definir las rectas que delimitaran los ángulos en el espacio de trabajo
La problemática con los ángulos comienza desde el inicio de los años escolares, por ejemplo, al realizar las tareas donde se necesitaba la creación de mapas, a la cual se le conoce como cartografía y es una ciencia de arte y calculo
Un dato interesante se puede observar en las pinturas de Leonardo da Vinci, ya que al ser analizadas, se puede identificar que el artista realizaba todas sus obras de arte sobre la base de cálculos matemáticos y el estudio de la proporción
En la vida cotidiana tenemos como ejemplo:
-La relación entre los ángulos y el plano
-Manecillas del reloj
-El movimiento de los pétalos de un girasol en dirección a la luz solar
Ejemplo:
-Un grupo de exploradores parte de un lugar L
-Camina un kilómetro hacia el sur
-Cambia de dirección 90°
-Recorre un kilómetro hacia el este
-Da vuelta nuevamente a la izquierda
-Se desplaza un kilómetro hacia el norte
-Sin embargo todos quedan desconcertados al darse cuenta de que han llegado nuevamente al punto de partida L
Solución
-Datos
-L es el lugar de partida
-Primer trayecto
-1 km al sur
-Segundo trayecto
-Giro de 90° y sigue 1 km al este
-Tercer trayecto
-Dobla a la izquierda y sigue 1 km al norte
-Análisis
-Al suponer que la tierra es una esfera y los exploradores están en movimiento, entonces la trayectoria descrita es un arco de meridiano en el movimiento al sur y un arco de paralelo en el movimiento hacia el este
-Síntesis interpretativa
-Con las definiciones se puede afirmar que si los excursionistas regresan al punto L, tomando un meridiano diferente del que han seguido al salir de L, dicho punto es el polo norte
-Hay que distinguir que el otro único lugar de la tierra en el que dos meridianos se encuentran es el polo sur, pero los exploradores no podrían haber salido de ese polo, para eso deberían haberse desplazado inicialmente hacia el norte