Área del circulo en Matemáticas 2
Si inscribimos en una circunferencia polígonos con diferente número de lados, el que tiene más lados se aproxima mejor su área a la del círculo
Para calcular el área de cualquier círculo se aplica la fórmula:
Ahora es necesario realizar un análisis geométrico que nos permite entender y demostrar que el área de cualquier círculo es la fórmula antes mencionada, analicemos la siguiente imagen: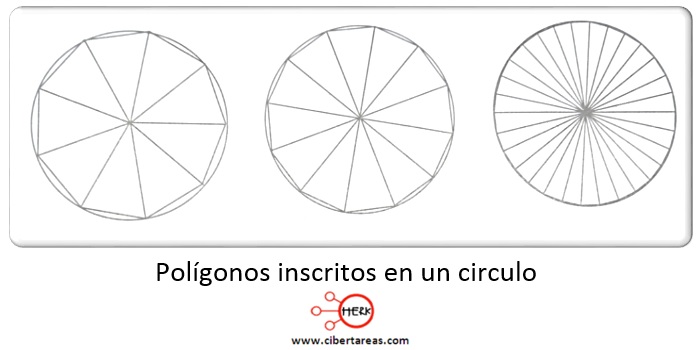
Al observar las imágenes anteriores, se pude apreciar que son diferentes y tienen varios lados, esta comparación visual ayuda a confirmar que en cuanto mayor sea la cantidad de lados del polígono, habrá una aproximación más fidedigna al área circular
La apotema de un polígono es el segmento que va del punto medio de cualesquiera de los lados del polígono al centro de la circunferencia circunscrita al polígono
Cuando se desenrollan los triángulos inscritos en el círculo, se genera un paralelogramo, con dimensiones de largo C y su altura es la apotema del polígono, esta es la mejor aproximación del radio del círculo
Al oponer triángulos se genera otro paralelogramo como el de la siguiente figura: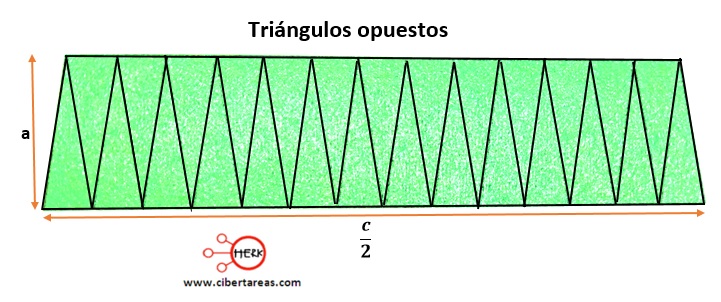
Con esto, las nuevas dimensiones son: altura, es decir, la apotema a, y de base, la mitad de la circunferencia (c/2)
Matemáticamente, se sabe que el área de un polígono es:
Donde:
– P
-Es el perímetro y se escribe como nk
– n
-Es el número de lados del polígono
– k
-Es la medida de cada lado
Cuando se da el caso de que n es muy grande, el apotemas e aproxima a tiende a r
Así con lo anterior, cuantos más lados tenga el polígono, más próximo se está de la circunferencia o perímetro
Entonces 
, solo si n tiende a ser muy grande, en otras palabras tiene muchos lados
: pero C es el perímetro de la circunferencia (C = π D = π 2r)
Sustituyendo:
El área de un círculo se obtiene del producto de π por el cuadrado del radio
