El Cálculo de Máximos y Mínimos en el Criterio de la segunda derivada en Cálculo Diferencial, concluyendo con el segundo método para calcular los máximos y mínimos de una función y=f(x):

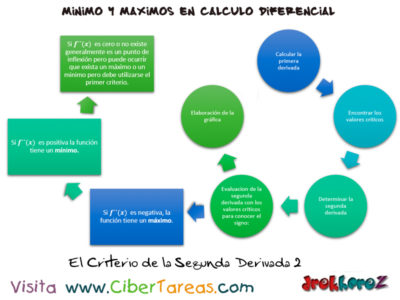
1.-Calcular la primera derivada
2.-Encontrar los valores críticos
3.-Determinar la segunda derivada.
4.-Evaluar la segunda derivada en cada un de los valores críticos para conocer el signo de ésta.

4.1.- Si f´´(x) es negativa la función tiene un máximo.
4.2.- Si f´´(x) es positiva la función tiene un mínimo.
4.3.- Si f´´(x) es cero o no existe generalmente es un punto de inflexión pero puede ocurrir que exista un máximo o un mínimo y en ese caso es mejor utilizarlo en el primer criterio.

5.-Elaboración de la gráfica correspondiente