Notación científica – Física 1

Hay que considerar que en la naturaleza existen objetos:

-Pequeños

-Como los quarks

-Muy alejados de la Tierra

-Como la galaxia Andrómeda

-Cuya duración es muy corta

-Como la vida de las partículas menos estables

-Cuya duración es muy larga

-Como la vida del Sol

-Con una masa tan pequeña

-Como la del átomo de hidrógeno

-Con una masa tan grande

-Como la de Saturno

Sin embargo existen formas de expresar una distancia muy grande o una muy pequeña, por ejemplo:

-El radio de un protón es del orden de 0.000 000 000 000 001 m

-La galaxia Andrómeda se encuentra a 10 000 000 000 000 000 000 000 m de distancia de la Tierra

Para estos casos surge la necesidad de aplicar la notación científica: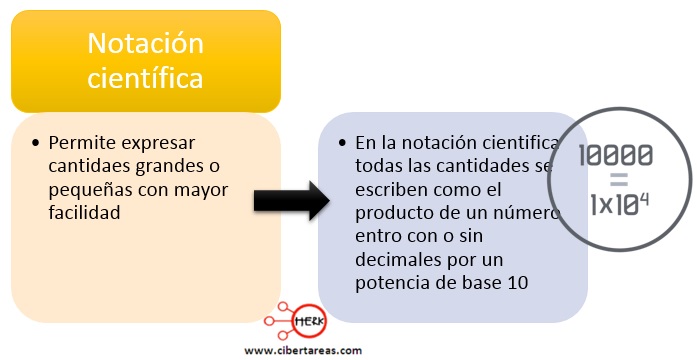

Es importante recordar que cuando un número se eleva a una potencia, ésta nos indica las veces que el número se multiplica por sí mismo, ejemplo:

Analizando el ejemplo anterior:

-Los números 2, 3 y 5 corresponden a los exponentes de la base 6

-El primer 6 está elevado a la segunda potencia, mientras que en el tercer 6 está elevado a la quinta potencia

Para el caso de las potencias de base 10, siempre será el 10 el que esté elevado a una potencia, por ejemplo:

Analizando el ejemplo anterior:

-En cada caso, la base 10 está elevada a una potencia positiva, el resultado es igual al número uno (1) seguido de tantos ceros como indique la potencia (exponente)

-Si el número 10 está a la sexta potencia (10⁶), se puede escribir este número como 1 000 000 (como un uno seguido de seis ceros)

En otro caso, para expresar cantidades pequeñas hay que elevar la base 10 a un número negativo, esto equivale a dividir 1 entre 10, elevado a esa misma potencia pero con signo positivo, por ejemplo: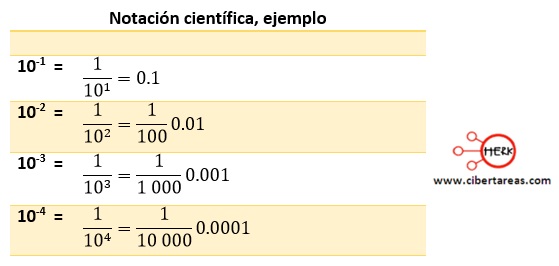

Analizando el ejemplo anterior, tenemos que:

-Cuando la base 10 está elevada a una potencia negativa, la cantidad se puede expresar como un número decimal, en donde el punto decimal a partir de uno se recorre hacia la izquierda tantas veces como lo señale la potencia negativa (exponente)

-Por tanto, 10^-6 se puede expresar como 0.000 001 (el punto decimal se recorrió seis posiciones de derecha a izquierda a partir del uno)

-10^-3 se puede expresar como 0.001

Tenemos que en la notación científica 4 X 10³:

-Significa que hay que multiplicar el 4 por 10³, como se observó en los ejemplos anteriores, es igual a 4 x 1 000 (el uno seguido de tres ceros)

-De igual manera, 4 x 10³ = 4 x 1 000 = 4 000

En la siguiente tabla se pueden observar algunas medidas de longitud expresadas en notación científica: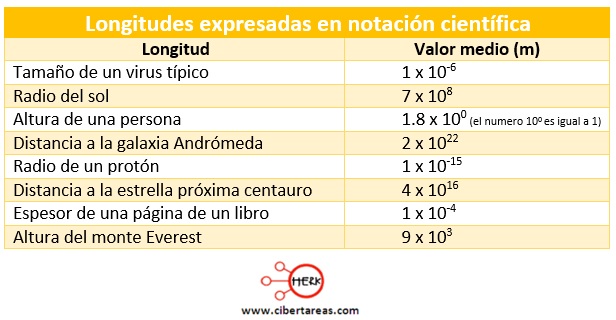

Cuando se realizan cálculos con números expresados en notación científica, se debe considerar lo siguiente:

-Suma de números expresados en notación científica

-Para que se puedan sumar o restar dos o más números expresados en notación científica, deberán tener el mismo exponente (misma potencia)

-El resultado se obtiene de sumar o restar (según sea el caso) los factores de las potencias y de multiplicar este resultado por la potencia correspondiente de base 10

-Por ejemplo:

-Es necesario sumar 3 X 10⁴ con 5 x 10⁴

-Se suman los factores de las potencias de base 10 (3 + 5), ya que ambos tienen la misma potencia, de manera que el resultado se puede expresar como:

3 X 10⁴ + 5 x 10⁴ = (3 + 5) X 10⁴ = 8 x 10⁴

-Multiplicación de números expresados en notación científica

-Se multiplican los factores de las potencias de base 10

-Luego, a dicho resultado se le multiplica por la base 10 con un exponente que resulta de sumar los exponentes de las potencias de ambos números

-Por ejemplo:

-Al multiplicar 3 x 10⁴ con 2 x 10⁵ el resultado es igual a:

 (3 x 10⁴)(2 x 10⁵) = (3 x 2)(10⁴)(10⁵) = 6 x 10^{4 + 5} = 6 x 10⁹

-División de números expresados en notación científica

-Se dividen los factores de las potencias de base 10 y dicho cociente se multiplica por la base 10 con un exponente que se obtiene de restar el exponente del divisor del exponente del dividendo

-Por ejemplo:

-Al dividir 4 x 10⁶ entre 2 X 10³ el resultado es:

-Raíz cuadrada de números expresados en notación científica

-El exponente debe ser un número par; si no es así, se hace el cambio correspondiente para obtener un exponente par

-Lo primero que se hace es extraer la raíz del factor de la potencia de base 10, después se multiplica dicho resultado por la base 10 con un exponente que resulta de dividirlo entre dos

-Por ejemplo:

-Raíz cuadrada de 81 x 10⁴ es igual a:

Ejemplo de notación científica

-Problema

-Es necesario calcular el área de una lámina rectangular

-Información

-Largo: 3 x 10⁴ cm

-Ancho: 2 x 10³ cm

-Formula

-Área de un rectángulo

A = a x b

-Solución

-Datos

b = 3 x 10⁴ cm

a = 2 x 10³ cm

A = ?

-Sustitución

A = 82 x 10³)(3 x 10⁴)

A = (2 x 3)(10³ x 10⁴)

A = 6 x 10³⁺⁴

-Resultado

A = 6 x 10⁷ cm²