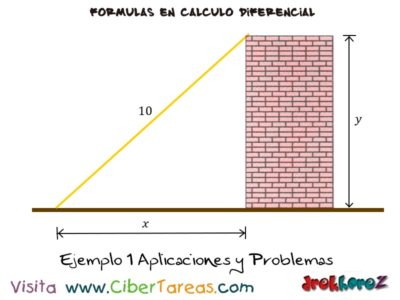
Las Aplicaciones y los Problemas como ejemplos en Cálculo Diferencial, vamos con un ejemplo sobre la figura de la escalera que está deslizando sobre el piso a razón de 3 pies/s.

¿A qué velocidad se desliza la parte de arriba de la escalera en el momento en que la base está a 8 pies del muro?

¿Cuál es el valor de dy/dt cuando dy/dt y x =8?

Valor del teorema de Pitágoras nos da la relación:

x² + y² = 10² de donde y = √100-x²

Al derivar x² + y² = 10² con respecto al tiempo tenemos:

2x dx/dt + 2y dy/dt = 0

Al despejar:

dy/dt = – 2x/2y dx/dt = – x/y dx/dt

Al Sustituir:

dy/dt = – x/ √100-x² dy/dx = – 8/ √100-8² (3)=- 4 pies/s

Al dejar caer una roca sobre un estanque en reposo al hacerlo produce ondas circulares concéntricas.En un radio de la onda exterior crece al ritmo constante de 1 pie/s.

El ritmo está creciendo el área de la es A = π r².

El crecimiento del radio es: dr/dt = 1 pie/s cuando r = 3.Ya que la varible independiente es el tiempo [t], de tal manera hay que derivar la variable área A con respecto al tiempo.

En el crecimiento del área es:

dA/dt = d/dt ( π r2) = 2π r dr/dt

Si r = 3 entonces:

dA/dt = 2π  (3)(1) = 6π r pie² /s