Calculo de valores 30°, 45° y 60° en Matemáticas 2
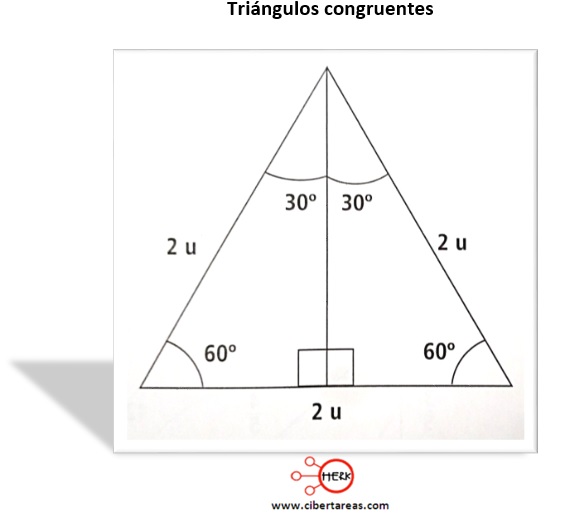
Para resolver esto, se debe de aplicar el teorema de Pitágoras para el desarrollo de estos cálculos angulares, en la siguiente figura se muestra un triángulo equilátero de lado 2 u, y un segmento que conecta el vértice superior y el punto medio de la base
Los dos triángulos congruentes son rectángulos, y tienen ángulos agudos con valores de 30° y 60°
Es importante mencionar que cada uno de los ángulos de un triángulo equilátero tiene un valor de 60°, así que si se divide unos de sus ángulos a la mitad, se tiene un Angulo de 30° en cada triangulo formado
Los valores de los ángulos internos de cada triangulo congruente son:
30° + 60° + 90° = 180°
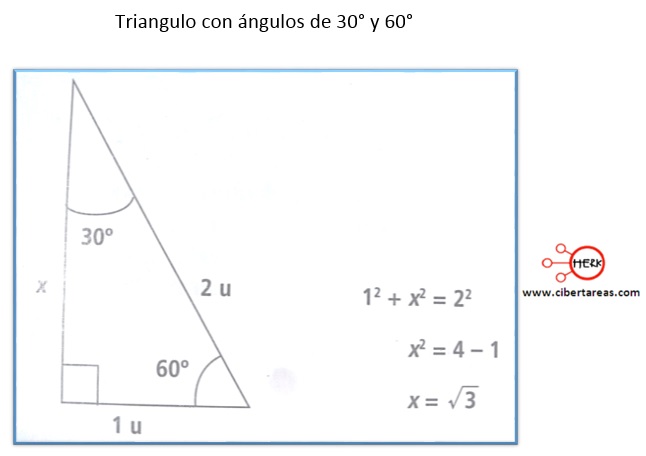
En el siguiente caso que se muestra en la figura, el cateto de la base mide 1 u y la hipotenusa 2 u
Por el teorema de Pitágoras tenemos:
Se toma como referencia el 
y se muestra que en el triángulo se cumple:
Para el caso de la tangente de 
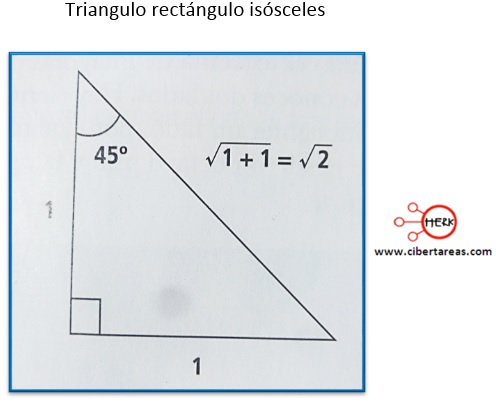
Al enfocarse en el triángulo rectángulo isósceles de la siguiente figura:
En este caso también se aplica el teorema de Pitágoras para hallar el valor de la hipotenusa
Para obtener el valor de coseno 45°, se sabe que coseno se describe como la relación entre cateto adyacente sobre hipotenusa, entonces:
El triángulo isósceles, además de mostrar dos lados con una misma magnitud, también tiene dos ángulos con iguales valores
