Funciones reciprocas en Matemáticas 2
Se habla de cantidades reciprocas cuando su producto es igual a la unidad, mediante el análisis de las seis funciones trigonométricas (seno, tangente, coseno, secante, cosecante, cotangente) se ve cuáles de ellas son reciprocas
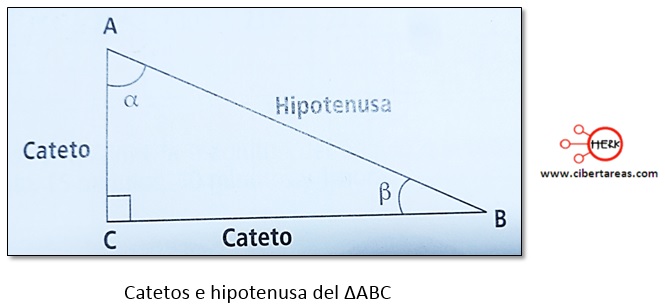
En el ∆ABC de la siguiente figura, se encuentran estas relaciones, las cuales también son de gran utilidad para la determinación de longitudes y ángulos
En el ∆ABC se puede apreciar que el ![]() es el adyacente
es el adyacente
Al comprar las magnitudes entre los catetos y la hipotenusa, se pueden definir seis razones trigonométricas:
Razón 1
-Cateto opuesto / hipotenusa
Razón 2
-Cateto adyacente / hipotenusa
Razón 3
-Cateto opuesto / cateto adyacente
Razón 4
-Cateto adyacente / cateto opuesto
Razón 5
-Hipotenusa / cateto adyacente
Razón 6
-Hipotenusa / cateto opuesto
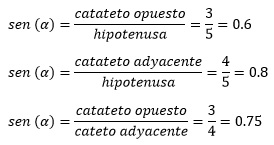
Al ejemplificar estas razones para tres relaciones especiales del ∆ABC, tenemos:
-Razón 1
-Razón 2
-Razón 3
Una forma de aprenderse estas relaciones es memorizar la palabra:
-SohCahToa
-Seno = opuesto/hipotenusa; Coseno = adyacente/hipotenusa; Tangente = opuesto/adyacente
Ejemplo
-Es necesario buscar las razones trigonométricas de una sombra triangular que produce un árbol
-Analicemos la siguiente imagen: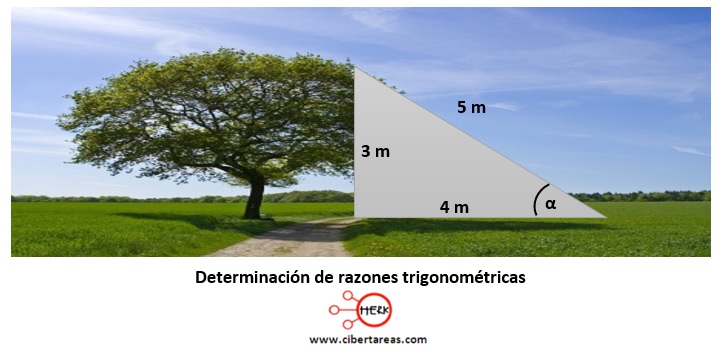
Solución
-Datos
-Cateto opuesto = 3
-Cateto adyacente = 4
-Hipotenusa = 5
-Análisis
-Síntesis interpretativa
– Es importante que se conserve las relaciones establecidas para cada función trigonométrica, así se podrá hallar su valor correcto
En este ejemplo, se ha utilizado solo tres razones de las seis que existen, esto ha sido posible porque todas están íntimamente relacionadas
En la siguiente tabla se pueden observar las relaciones de las seis funciones: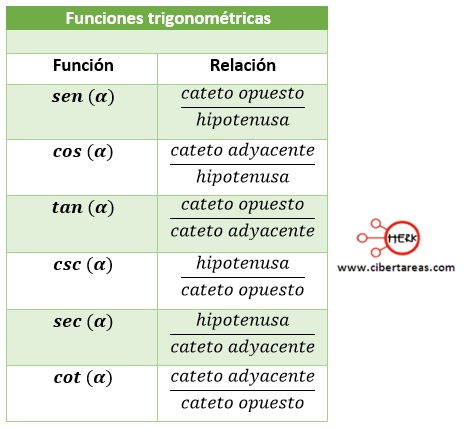
La siguiente figura permite determinar las funciones reciprocas en un triángulo rectángulo, a partir de un valor de α de un ángulo agudo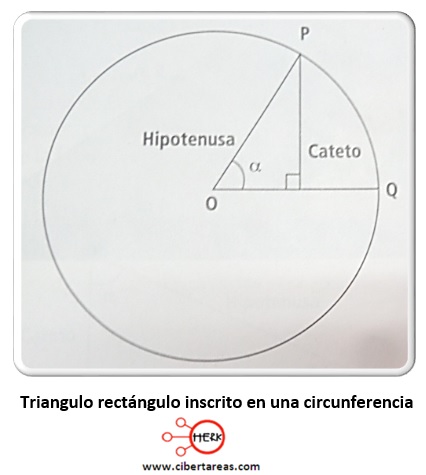
Cuando se desplaza el punto P sobre la circunferencia, se hace varia el calor para α, y su referencia permite definir las seis funciones
Al tomar seno como ejemplo, tenemos como su función inversa (1/seno) permite mostrar que se trata de la cosecante:
La función reciproca se obtiene de las siguiente manera:
A esta nueva función se le llama función cosecante y se denota como:
Análogamente, se puede definir las siguientes funciones:
Estas nuevas funciones son llamadas las funciones reciprocas de sen (α), cos (α) y tan (α), respectivamente
Cabe destacar que son funciones reciprocas para un mismo ángulo agudo:
-Seno y cosecante
-Coseno y secante
-Tangente y cotangante