Componentes de un vector en Física 1

Debemos considerar que el concepto componentes vectoriales es muy importante en física, ya que ayuda a comprender situaciones cotidianas y fenómenos que ocurren en la naturaleza

Tenemos dos líneas de acción que se deben considera, es posible:

1.-Sustituir dos o más vectores por un vector resultante que provoque el mismo efecto que éstos

2.- Descomponer un vector cualquiera en componentes, de manera que éstas produzcan el mismo efecto que el vector que sustituyen

Las componentes de un vector actúan en direcciones distintas de la del vector:

Una de las características fundamentales de las componentes es que su suma es igual al vector original:

Las componentes de un vector se pueden utilizar en lugar del mismo vector en cualquier cálculo que convenga hacerlo, las componentes de un vector de mayor interés son:

Componentes cartesianas

-Son las más utilizadas

-Corresponden a las proyecciones del vector sobre los ejes del sistema de coordenadas cartesianas

-Estas componentes forman un ángulo recto entre sí, se les conoce también como componentes rectangulares

Las componentes rectangulares de un vector en dos dimensiones (en el plano) se determinan gráficamente trazando por el extremo del vector dos líneas perpendiculares a los ejes x y y del sistema de coordenadas, como se muestra en la siguiente figura:

Las componentes rectangulares de un vector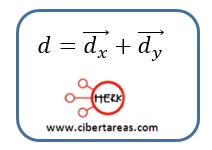

Al sumar gráficamente las componentes rectangulares y el vector original se forma un triángulo rectángulo:

A partir de la figura anterior y las funciones trigonométricas seno y coseno se pueden determinar matemáticamente las magnitudes de las componentes rectangulares:

Analizando la figura anterior se deduce que: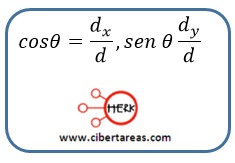

Por tanto, las magnitudes de las componentes rectangulares se obtienen de:

A manera de introducción, en el siguiente problema de ejemplo se muestra cómo aplicar las ecuaciones anteriores para determinar las magnitudes de los componentes rectangulares de un vector.

Ejemplo:

Problema

-Un vector que representa el desplazamiento

-Es necesario determinar las magnitudes de las componentes x y y de este vector

Solución

-Datos

-Formulas

-Sustitución

-Resultados

Ahora analicemos otro ejemplo o problema:

-Problema

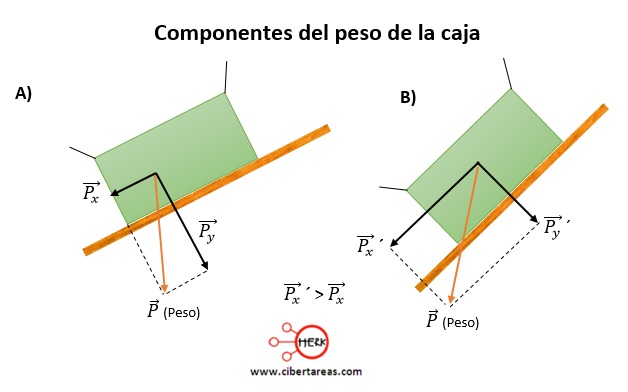
Es necesario saber por qué una caja se desliza más rápido en un plano más inclinado que en uno menos inclinado

-Solución

Si se consideran los componentes del peso de la caja que se desliza sobre los planos inclinados, podrá́ comprenderse la causa de que su rapidez dependa de la inclinación del plano

Observemos en la siguiente figura que a mayor inclinación del plano, más grande se vuelve la magnitud de la componente  y más rápido se desliza la caja

La componente