Suma de vectores en Física 1

Antes de abordar este tema, es importante señalar o recordar que la gran mayoría de las magnitudes escalares se suma de acuerdo con las reglas de la aritmética ordinaria, por ejemplo:

-Se tiene un balde con 3 kg de azúcar y después otro de 4 kg del mismo producto, al sumarlo se tendrá un total de 7 kg, el resultado se obtiene realizando:

3 kg + 4 kg = 7 kg

Para la suma de vectores se debe tomar en cuenta tanto la magnitud como su dirección y sentido, por ejemplo:

-Un escarabajo tiene un desplazamiento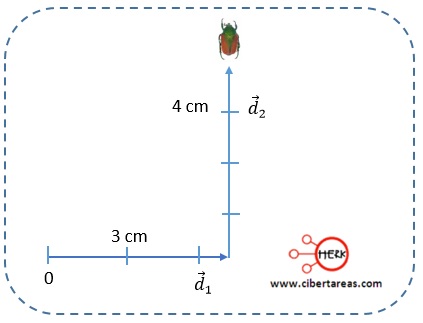 

-Si el desplazamiento fuera una magnitud escalar, se podría decir que el desplazamiento total del insecto fue de 7 cm, pero como el desplazamiento es una magnitud vectorial, el desplazamiento total del escarabajo tiene una magnitud de 5 cm, ya que dicho desplazamiento es un vector que va de la posición inicial del escarabajo al posición final de esté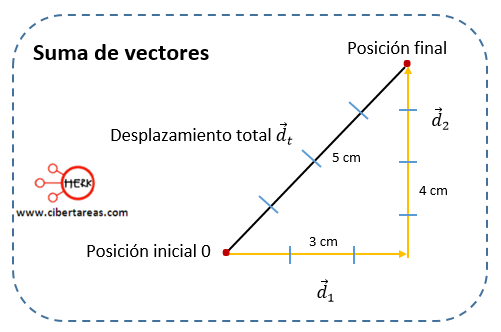

-El efecto final del desplazamiento total  y  de la misma

-Simbólicamente, la suma de los dos desplazamientos se representa por:

Cabe mencionar que la forma en que se sumaron los dos desplazamientos en el ejemplo anterior es válida para cualquier otra magnitud vectorial

Tenemos que sumar vectores consiste en: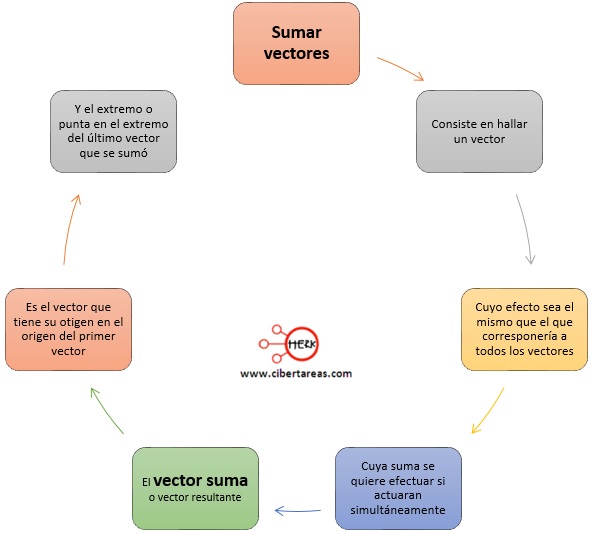

Es importante señalar que cuando se efectúa la suma de dos o más vectores todos deben tener las mismas unidades, es decir, no se pueden sumar vectores desplazamiento con vectores fuerza, y que cuando se sumen vectores desplazamiento (o vectores fuerza) deberán tener las mismas unidades

Existen métodos para sumar vectores, como:

-Métodos analíticos o matemáticos

-Métodos gráficos

Cuando los vectores son recurrentes, el método gráfico se conoce como método del polígono, por ejemplo:

1.- Representar las magnitudes vectoriales por medio de vectores (flechas) previa selección de la escala adecuada

2.- Con origen en un punto arbitrario del espacio (o en un punto determinado según el problema) se traza el primer vector, el cual se escoge arbitrariamente, y en el extremo de éste se dibuja el segundo vector, mismo que deberá conservar su magnitud, dirección y sentido, y cuyo origen deberá coincidir con el extremo del primero

3.- Continuar el procedimiento de unir el origen de cada nuevo vector con el extremo o punta del vector precedente hasta que todos los vectores del problema hayan sido dibujados

4.- Trazar el vector resultante o vector suma, de manera que su origen coincida con el origen del primer vector y su extremo con el extremo del último vector que se sumó

5.- Medir con regla y transportador la magnitud y el ángulo del vector resultante para expresar su valor y dirección de acuerdo con la escala seleccionada

Tenemos que el vector suma (resultante) o cualquier otro vector se especifica con frecuencia mediante un par de letras: R y θ

R

-Corresponde a la magnitud del vector

θ

-Corresponde a su dirección

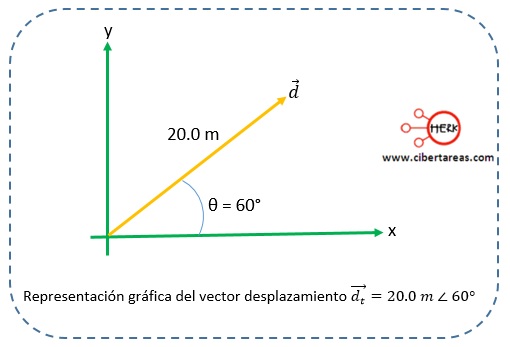
Debemos considerar que el ángulo θ se acostumbra medir a partir del eje x positivo y en sentido contrario a las manecillas del reloj, por ejemplo:

-Si el desplazamiento total de un cuerpo es de 20.0 m y forma un ángulo de 60° con la horizontal, el vector desplazamiento o, simplemente, desplazamiento se puede representar simbólicamente por las siguientes formas:

-De forma gráfica tenemos: