Continuidad en los Límites en Cálculo Diferencial definiremos e significado que es el mismo en lenguaje cotidiano.Es decir que una función (f) es continua en [x=a] debe entenderse como que su gráfica no sufre interrupción en [a] que no se rompe ni tiene saltos o huecos.

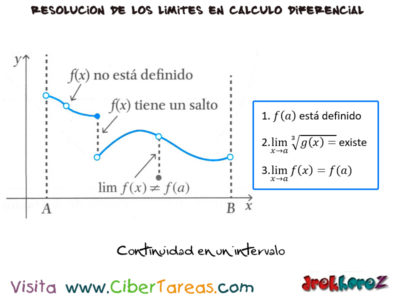
En la Continuidad en un intervalo: una función [f] es continua en un intervalo [A,B] si es continua en todo número del intervalo. En la siguiente figura se muestran tres valores de [x] en los que la función no es continua.

Los demás puntos del intervalo [A,B] la gráfica no se interrumpe y decimos que la función es continua en ellos.Para que una función se continua en [x=a] se requieren tres cosas mostradas en la siguiente imagen:

Un ejemplo claro en las siguientes Funciones continuas, según sea el caso contrario escribe los puntos de discontinuidad:

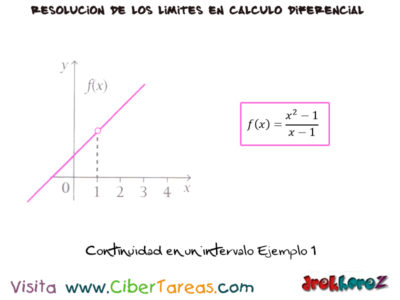
1.-Es obvio que la función del limite no esta definida en x=1

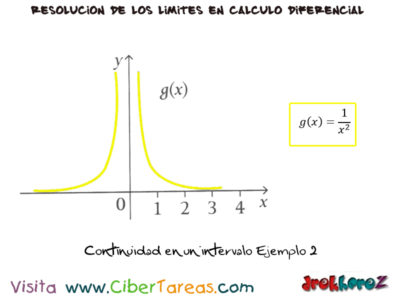
2.-La función no está definida en x=0 y además limite no existe.

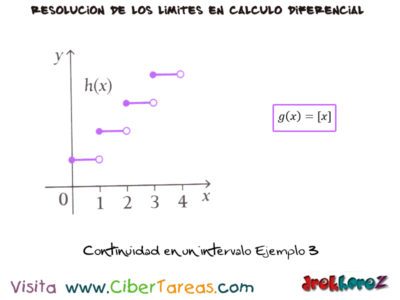
3.-La función mayor entero g(x)=[x] tiene discontinuidades en todos los enteros ya que limite no existe si [n] es un entero.