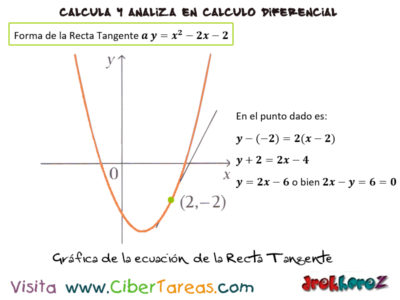
Ejemplo de la Tangente de una Curva como Aplicación de la derivada como razón de cambio en Calculo Diferencial, encontrando la ecuación de la recta tangente a la parábola y=x²-2x-2 en el punto (2,-2)

La derivada de la función y=x²-2x-2 es la pendiente de la recta tangente a la curva en el punto dado.En la siguiente imagen forma la ecuación de la recta tangente en el punto dado es.

y-(-2) = 2(x-2)

y+2=2x-4

y=2x-6 o bien 2x-y=6=0