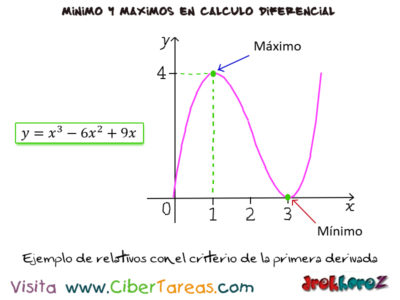
Ejemplos de calculo de máximos y mínimos relativos con el criterio de la primera derivada en el Calculo Diferencial en la función y=x3 – 6x2 + 9x y después elaborar la gráfica correspondiente.
Al calcular la derivada e la función:
dy/dx=3x2 -12x + 9
Igualamos a cero la derivada de la función:
3x2 – 12x + 9 = 0
Al factorizar y resolver la ecuación, tenemos que:
3 (x-3) (x-1) = 0
Entonces los valores críticos lo apreciamos en la siguiente imagen:
Observa que solo interesa los signos de la derivada, Como la derivada cambia de positiva a negativa concluimos que e el punto (1,4) hay un máximo relativo.
Análisis del valor crítico x2 =3
donde apreciamos en lo siguiente:
En la derivada cambia de negativa a positiva por lo que concluimos que en el punto (3,0) hay un mínimo relativo. Al trazar la gráfica de la función es relativamente fácil ya que es continua en todo su dominio. En el punto 1.4 existe un máximo la curva es concava hacia abajo.
Para el punto 3.0 hay un mínimo por lo que la curva es concava hacia arriba, En la tabla de los valores aprecias los puntos a la izquierda y a la derecha al uniros con una linea suave. La gráfica se obtiene en la siguiente imagen: