Elementos de los polígonos: radio, apotema y diagonal en Matemáticas 2
Es importante conocer los elementos de un polígono, los cuales son:
Las definiciones de tres elementos de un polígono son: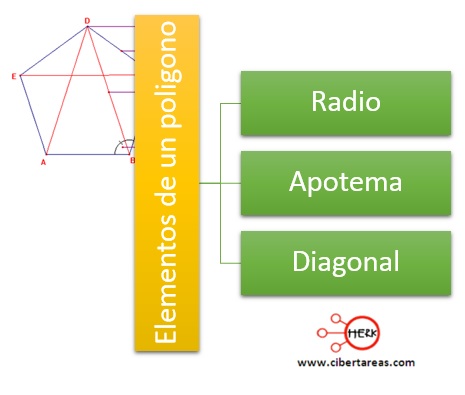
Radio
-Segmento lineal que une cualquier vértice con el centro del polígono
Apotema
-Segmento que une el centro del polígono con los puntos medios de sus lados
Diagonal
-Segmento que une dos vértices no consecutivos del polígono
Ejemplo
-Un grupo de cuatro personas intercambian un apretón de manos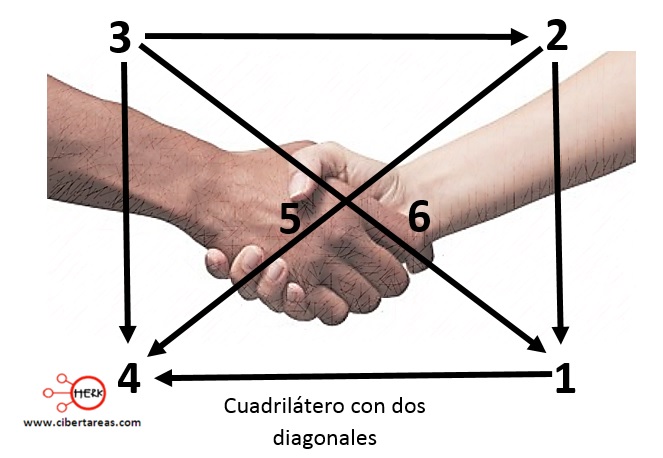
-¿Cuántos saludos se dieron?
Solución
-Datos
-Cuatro amigos
-Cantidad de saludos = ¿?
Análisis
-Una persona da tres saludos
-La segunda, dos
-La tercera da uno solo
-Es decir: 3 + 2 + 1 = 6
-Es importante observa que el número de diagonales es el resultado del número de intercambios menos el número de lados del polígono (para este caso 4), es decir:
6 – 4 = 2
-Para un caso de cantidades mayores de personas, tenemos:
-6 personas
-Se cumple el patrón anterior:
5 + 4 + 3 + 2 + 1 = 15
-El número de diagonales se obtiene tal como en el caso de las cuatro personas
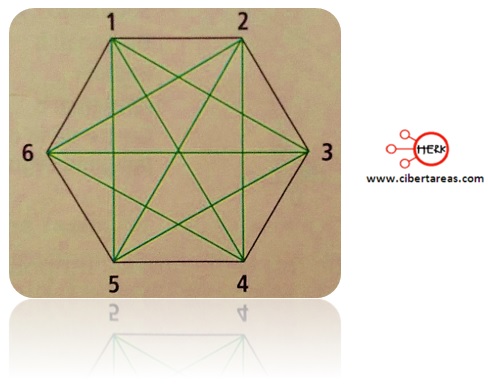
-En la siguiente figura se debe considerar que ahora se trata de un hexágono:
-7 personas
-El número de intercambios sería:
6 + 5 + 4 + 3 + 2 + 1 = 21
-El número de diagonales:
21 – 7 = 14
Síntesis interpretativa
-Para el primer caso se obtuvieron 6 intercambios y al analizar estas conexiones a nivel geométrico se definieron ciertas características de los polígonos
-Existe otra forma de encontrar la suma para los intercambios de saludos, como en el caso del ejemplo anterior, es el mecanismo propuesto por el matemático Carl Gauss parar sumar números enteros consecutivos
-Para 10 intercambios se tiene: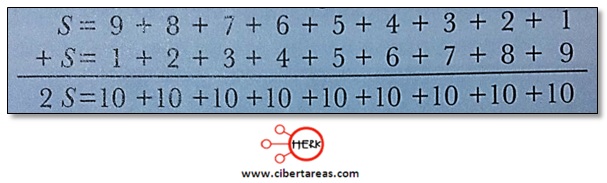
Es importante mencionar que el número 10 se repite 9 veces
La igualdad anterior se pude simplificar del siguiente modo:
En consecuencia, el número de diagonales de un polígono de 10 lados seria:
Realizando un análisis más concreto, ahora hay que ir de lo particular a lo general, y se debe deducir una fórmula para encontrar las diagonales para saber cuántas diagonales hay en un polígono de n lados, la respuesta sería:
La fórmula anterior consiste en el número de intercambios de saludos menos el número de lados del polígono
Si se desea emplear el método de Gauss, se puede encontrar la fórmula general que determina las diagonales de un polígono, para obtener los intercambios de saludos entre n amigos, debemos restarle al total de intercambios el número de lados que tiene el polígono formado en el intercambio de conexiones
Es importante que n se repite (n – 1) veces, entonces se pude sintetizar la expresión anterior de la siguiente forma:
La fórmula anterior permite sumar números enteros consecutivos, y el número de diagonales se obtiene con la siguiente formula: