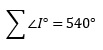Suma de ángulos interiores y exteriores de un polígono en Matemáticas 2

Si se considera que un polígono es una organización de triángulos inscritos, se puede considerar los ángulos interiores o internos y exteriores o externo, es importante mencionar que la suma de los ángulos internos de cualquier triangulo es de 180°

Para T₂, sus valores deben cumplir la propiedad: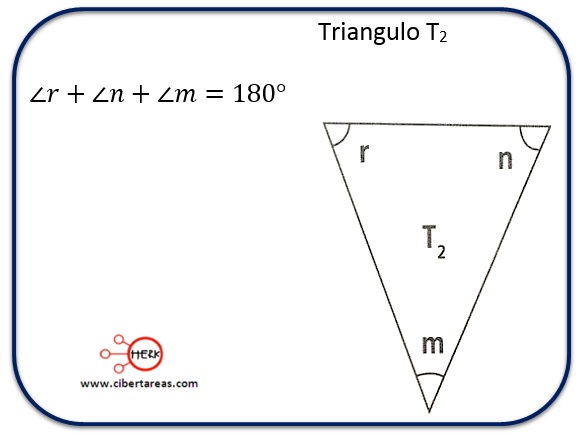

Tenemos que para determinar el total de la suma de los ángulos internos de un polígono de n lados se emplea la fórmula:

Donde:

∑ es la sumatoria de todos los ángulos internos

-Ejemplo:

-Para un triángulo definimos:

Para encontrar el valor de cada ángulo interno de un polígono regular se emplea la fórmula:

-Ejemplo:

-Para el caso de un triángulo equilátero se tiene:

Para el caso de los ángulos externos, analizando la siguiente figura:

Tenemos que se pueden apreciar los ángulos exteriores del triangulo

Ahora vamos a analizar que sucede con el triángulo y sus ángulos, si se utiliza una regla y transportador para hacer un trazo y se desplazan los ángulos del triángulo de la figura anterior, se puede observar que la suma de los tres ángulos sigue siendo 360°, ejemplo: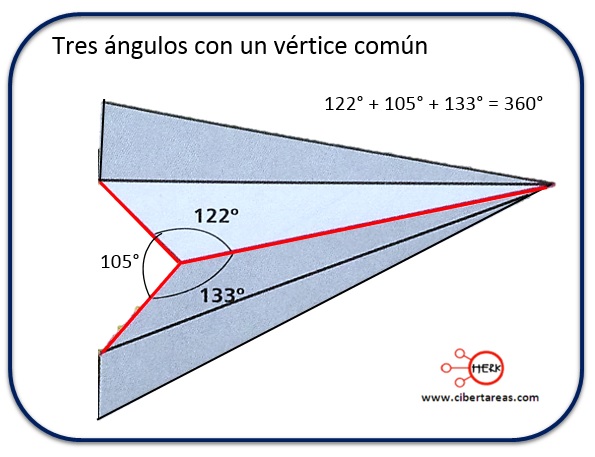

Como ejemplo tenemos:

-Es necesario determinar qué tipo de figura geométrica tiene un total de 540° en sus ángulos internos

Solución

Datos

N= ¿?

Análisis

-Se recurre a la fórmula que describe la suma total de los ángulos internos y se despeja la varíale n, tenemos: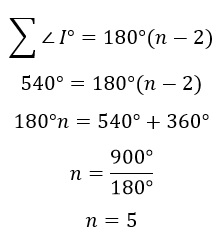

Síntesis interpretativa

-El valor de n=5 indica que la figura es un pentágono

Veamos otro ejemplo:

-Tenemos que los ángulos exteriores del pentágono irregular de la siguiente figura son números consecutivos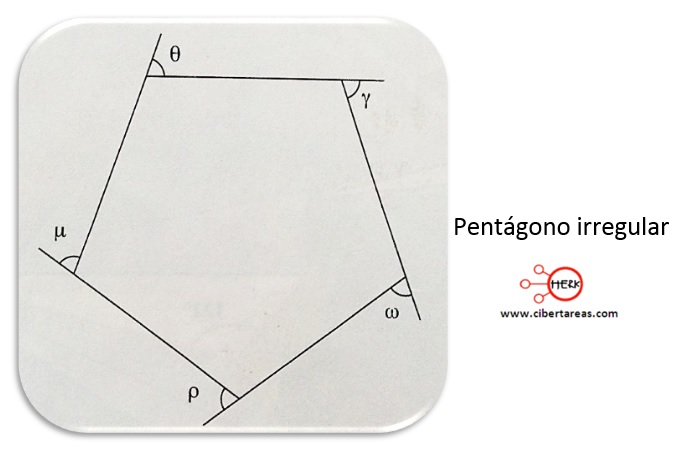

-Es necesario calcular el valor de cada ángulo

Solución

-Datos

-Es un pentágono

-Sus ángulos externos son µ, θ, ϒ, ɯ, ƿ

-Análisis

-Los ángulos son valores consecutivos, por lo tanto se fija un valor, por ejemplo:

θ = n

-Al ser consecutivos, el siguiente valor es

ϒ = (n + 1)

-Y así sucesivamente

-Entonces se pude formular:

-Con esto se obtiene una ecuación de primer grado n, y su solución permite encontrar los valores de cada ángulo exterior

-Si se suman los términos semejantes y se resuelve para n, se tienen:

Síntesis interpretativa

-Al obtener el valor para n, podemos definir los binomios que se suman al monomio n ara dar el total de 360°