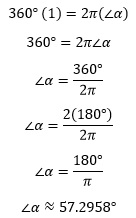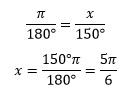Conversión de ángulos en grados a radianes y viceversa en Matemáticas 2
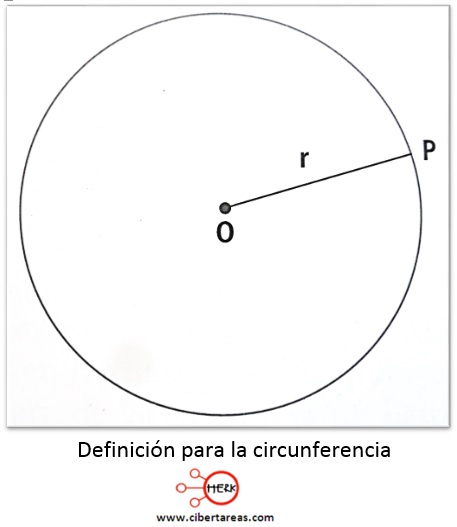
En el círculo de la siguiente figura se observa la magnitud de la circunferencia en términos de r
La circunferencia se determina por la función:
C(r) = 2πr
Cuando el radio es igual a 1, se obtiene la circunferencia unitaria, la cual es: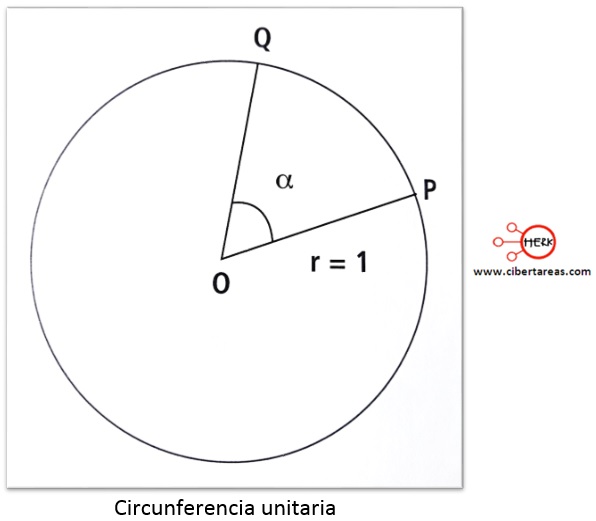
A partir de la circunferencia untaría se puede definir las siguientes conclusiones:
1.- El ángulo central 
, adquiere distintos valores determinados por la posición del punto Q
-Si Q coincide con P, entonces 
-Si 
4 = 90°
-De manera intuitiva se tiene que 
adquiere un valor mínimo cuando P coincide con Q, y un valor máximo (360°) cuando Q recorre toda la circunferencia y vuelve a coincidir con P
2.- La longitud de la circunferencia unitaria es: C(1) = 2π Cuando se desplaza a Q sobre la circunferencia, se determina un arco que una fracción de 2π
-Si 
, entonces se determina una longitud de 2π
-Si 
-Si, 
Se puede asociar la magnitud del arco en función de la apertura de
Como se menciono anteriormente, cuando en la circunferencia unitaria , el arco tiene una magnitud igual a 2π, por lo que la siguiente relación de proporcionalidad se cumple:
Esto arroja un resultado interesante:
Este resultado ha recibido un nombre:
-Radian
-Su símbolo es rad
Con el dato anterior se pude formalizar la conversión de grados a radianes, es decir: 
y así sucesivamente
Las transformaciones de ángulos en grados a radianes y viceversa siguen unas operaciones muy sencillas:
Caso 1
-Grados a radianes
Se toma como ejemplo 150°
Caso 2
-Radianes a grados
Se toma como ejemplo
Con la descripción de estos dos casos, se puede comprobar las relaciones que se dan entre ángulos y radianes en la siguiente tabla:
Caso 3
-Minutos y segundos a grados
Algunas veces se puede encontrar valores de minutos y segundos asociados con los ángulos, para estos casos se pasan dichos valores a la fracción de grados respectiva, por ejemplo:
La aplicación de los radianes y ángulos para determinar longitudes se practicó desde épocas anteriores a nuestra era, como es el caso de:
-Tales de Mileto
-Matemático griego
-Hallo la altura de las pirámides de Egipto a partir de la sombra triangular que proyectaba un lado de la pirámide
