Funciones trigonométricas para ángulos de cualquier magnitud en Matemáticas 2
En este tema van implícitos varios conceptos relevantes dentro de las matemáticas como:
-Funciones
-Ángulos de referencia
-Periodicidad
-Identidades
-Puntos de correspondencia
-Gráficas y sus interpretaciones
Para entender estos ejercicios trigonométricos se debe recurrir constantemente a los conocimientos geométricos
El estudio de este tema es útil para el cálculo de longitudes y ángulos, sino que también ofrece una explicación de los conceptos relacionados con la vida cotidiana, por ejemplo, en la música, ya que las notas de cada instrumento se describen como ondas sinusoidales con ciertas frecuencias y amplitudes
Existen diversos contextos que permiten reconocer el concepto de función en la vida diaria, al observar el medio ambiente donde nos desenvolvemos, se puede apreciar ciertas relaciones interesantes, como:
-Estatura
-Peso
-Color de ojos
-Color de cabello
-Longitud de brazos, etc.
En el ámbito geométrico se pude hacer transformaciones, por ejemplo:
-A partir de ciertos datos asociados con el perímetro se puede definir el área y a la inversa
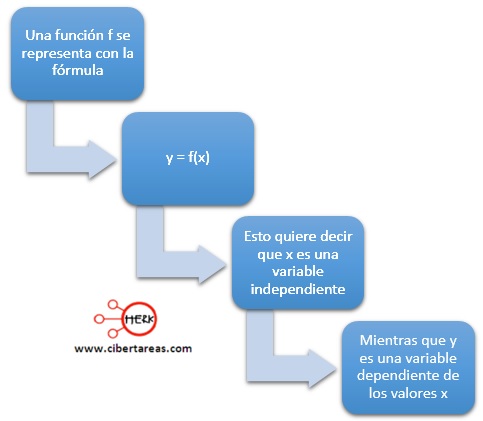
-Para lograr lo anterior, se debe realizar una transformación que consiste en establecer una regla o correspondencia entre elementos de dos conjuntos
-A esta relación mencionada se le define como función
-Es de suma importancia que se reconozca que toda función tendrá una variable dependiente con el condominio y otra dependiente en el dominio
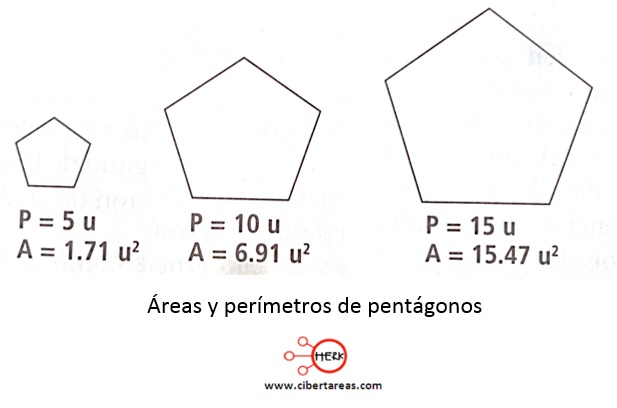
En la siguiente figura se muestran tres pentágonos con sus respectivos perímetros y áreas
Es importante considera que en la sucesión de valores presentes en estos polígonos existe alguna relación, y los elementos de estos polígonos ayudan a establecer una función entre el perímetro y el área
En la siguiente imagen se puedo observar a estas parejas de valores a dos distintos conjuntos: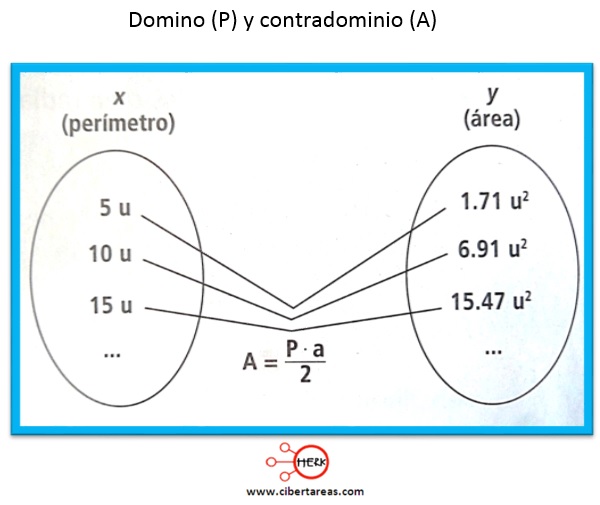
En esta imagen se puede notar la relación uno a uno que se establece a través de una regla de correspondencia
Al seguir esta pauta se transforma un conjunto de calores que constituyen el perímetro, y que para este caso se refieren al dominio de la función
El conjunto transformado bajo la regla de correspondencia recibe el nombre de contradominio o imagen de la función, que para este caso es el área
La transformación se logra por la regla que pone en relación el área (A), el perímetro (P) y la apotema (a), tenemos:
A = Pa/2
En la función existe un arreglo de parejas ordenadas en el que cada elemento del dominio solo se relaciona una única vez con un elemento del contradominio, si un elemento del domino se relaciona más de una vez con otro elemento del contradominio, se habla de una relación
La transformacion consiste en multiplicar el perimetro por su apotema respectiva y dividir el rodocto entre dos, así se obtiene el area, esto se muestra como una pareja ordenada (P, A)
A manera de sintesis, se forma el siguiente arreglo: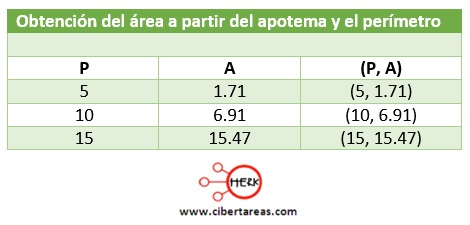
Al aplicar la formula para el área: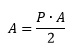
Se puede confirmar que para el perímetro de 5 unidades de medida (u) y la apotema de 0.684 que aparecen en la tabla anterior, el área sera: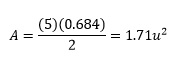
Existe un gran numero de reglas de correspondencia que generan funciones, por ejemplo:![]()
Para este tema se trabajar las funciones trigonométricas:
Las funciones que llevan una “r” como subindice con las reciporcas, es estas funciones, x puede tener un vaor en grads o en radianes
Ejemplo:
Para F(x) = sen (x), si x = 0°, x = 15°, x = 30°, x = 45°, es necesario obtener sus valores y realizar uan representacion del dominio y codominio con la funcion respetiva
Solucion
-Datos
f(x) = sen (x)
x = 0°
x = 15°
x = 30°
x = 45°
-Análisis
-Al utilizar una calculadora científica, se incluye los cuatros grados respectivos y se obtienen sus valores para seno, tenemos que para obtener el resultado para sen (15°):
1.- Se oprime la tecla sin
2.- Se escribe el numero 15
3.- Se presiona la tecla de igual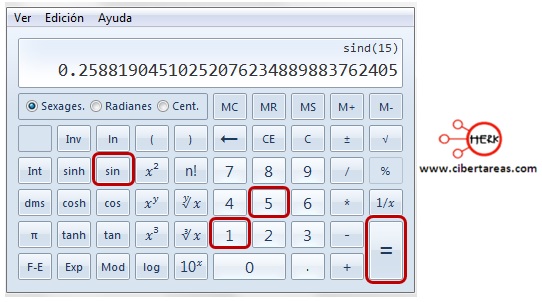
El resto de los resultados es:
f(x) = se (x)
sen (0°) = 0
sen (15°) = 0.2588
sen (30°) = 0.5
sen (45°) = 0.7071
Con estos datos ya se puede organizar el conjunto de valores para el codominio: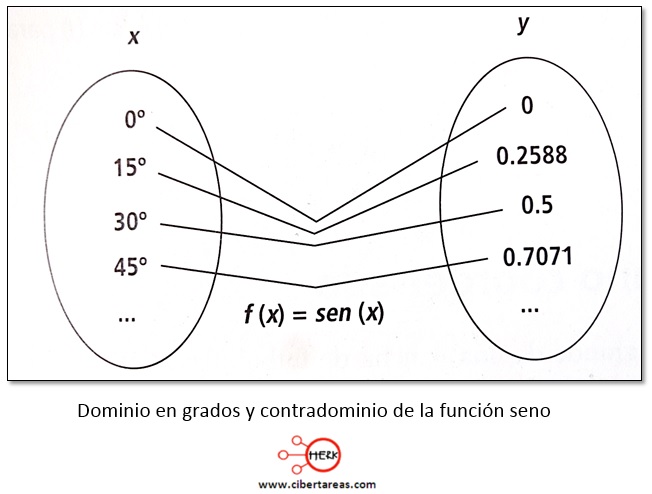
-Síntesis interpretativa
-Se puede ver que conforme surge un aumento de grados, también hay un incremento en el valor de los datos que resultan de la función seno, al menos en este rango de valores