Gráfica de la función tangente en Matemáticas 2

A partir de la siguiente figura se deben establecer las relaciones trigonométricas para el ángulo de referencia β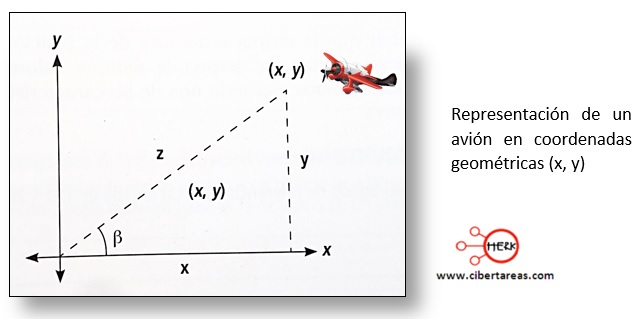

La función tangente se define como: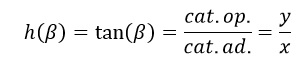

Para las funciones seno y coseno tenemos: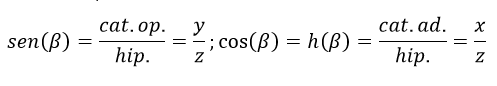

A partir de lo anterior, se puede observar cómo se vinculan seno y coseno con la tangente: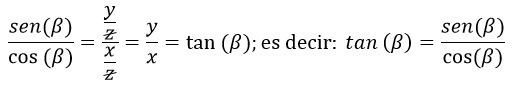

Es importante mencionar que una expresión trigonométrica se puede representar de varias formas, hay que recordar que se tiene un marco circulas como referencia

Para encontrar los valores de la función tangente y construir su gráfica, se completa la siguiente igualdad: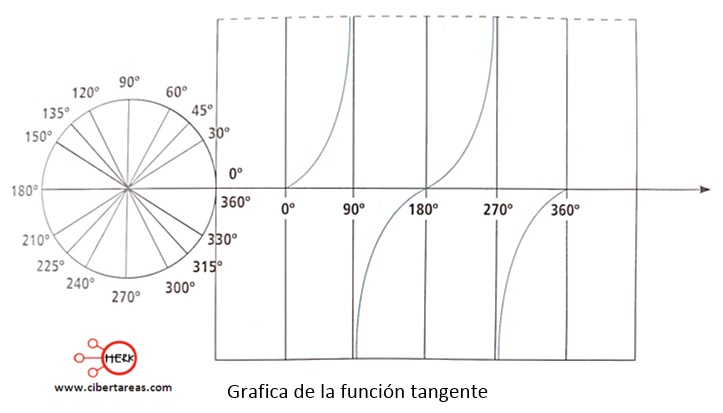

En la siguiente tabla se indican los datos donde la gráfica adquiere valores ±1 o 0, o no existentes (esto se da cuando el denominador es cero, es decir, cuando el valor del coseno del ángulo en cuestión es cero)

Es importante recordar que la división no está definida cuando el denominador es cero, en esos casos se tendría que decir que no existe ese valor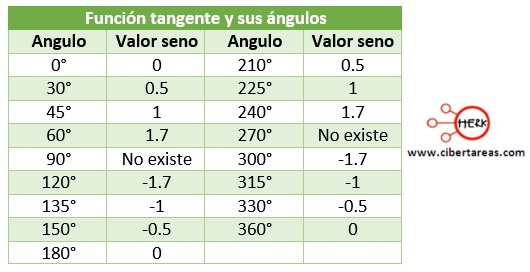

En los valores donde no existe contradominio, no hay continuidad en la gráfica de la función,  es decir, no es un trazo continuo

En la siguiente gráfica se observa la función tangente:

La función tangente no está definida para 90° y 270°, es decir, no está definida para ángulos de la forma para n = 0, 1, 2, …

Las características de la función tangente son peculiares con respecto a las funciones seno y coseno, tenemos:

-La función tangente presenta discontinuidades en los ángulos de 90° y 270°

-Al teclear en la calculadora científica tan (90°) o tan (270°), marcara ERROR, e esto se debe a que implícitamente se está intentando dividir entre cero

-La función es periódica, es decir:  , de periodo k, para esta caso k = 180°, por ejemplo: tan (45°) 0 tan (45° + 180°)

La función corta el eje de las x cada 180°, a partir de 0°