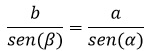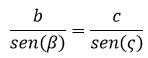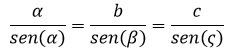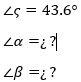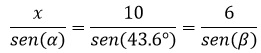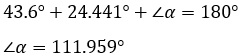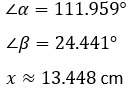Ley de senos en Matemáticas 2
Para este tema, tenemos que analizar el siguiente ejemplo, en donde el análisis trigonométrico para el caso de un triángulo perite mostrar esta ley
Ejemplo:
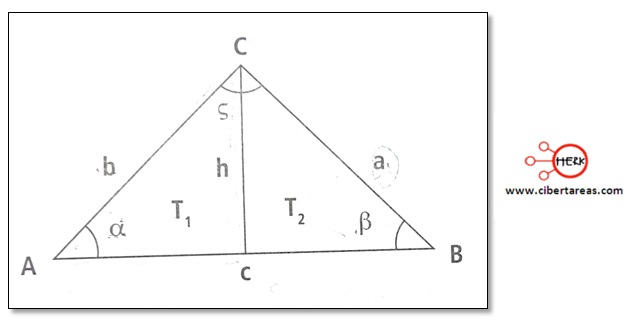
-Se considera el 
que tiene sus lados opuestos con longitudes a, b y c, respectivamente, como se muestra en la siguiente figura:
-Es importante saber cómo se trazaría un segmento perpendicular al lado y que pase por le vértice A así mismo que conforme por construcción dos triángulos rectángulos T1 y T2
-Se denota por h a la altura, se debe obtener el seno para 
Solución
-Datos
Lados a, b y c
Vértices A, B y C
-Análisis
-Para 
-Para 
-Como h = h, entonces también:
-Conformamos una proporción:
-Al cambiar la altura de referencia del triángulo y se traza el segmento k que paso por el vértice A y es perpendicular al lado a, se forman dos triángulos T3 y T4, como se muestra en la siguiente figura, y que por construcción son rectángulos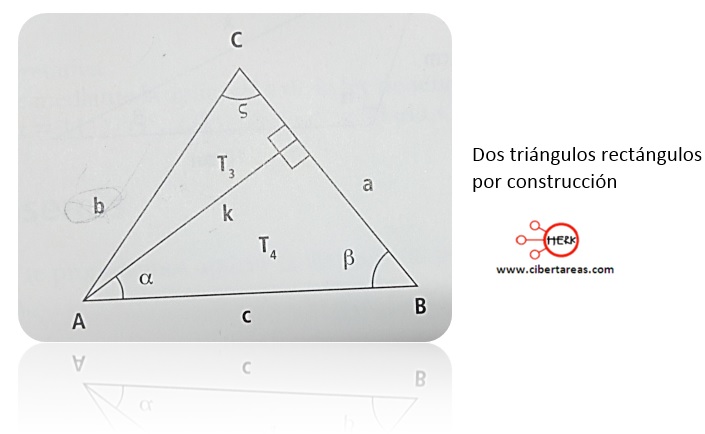
-Se obtiene el seno para 
-En T3:
-En T4:
-Nuevamente, como k = k, entonces:
-Se conforma la proporción:
-En los triángulos T1 y T2 se obtiene la relación:
-De este modelo se pude estructurar una tripe igualdad:
-Síntesis interpretativa
-A estar relación se le denomina ley de senos
-En la práctica al aplicar esta ley, implica identificar los elementos de la fórmula con el contexto de cada problema o ejercicio y realizar las operaciones correspondientes
Ejemplo
-Es necesario encontrar los valores de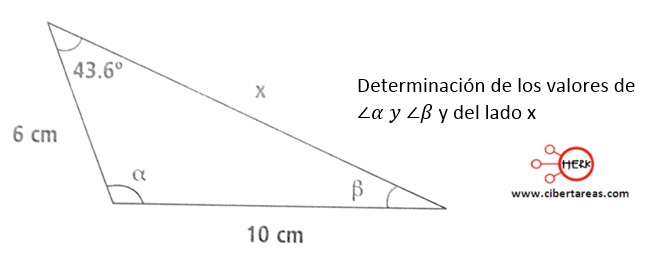 
Solución
-Datos
Lados = 6 cm, 10 cm
x = ¿?
-Análisis
-El triángulo es oblicuángulo, y de acuerdo con la ley de senos, sabemos que:
-Ahora se debe encontrar primeramente el valor para :
-Si tenemos los valores de dos ángulos, se pude obtener el tercero ():
-Ahora se debe de encontrar el valor del lado x, para esto debemos resolver:
-Síntesis interpretativa
-Con esto se observa que mediante la aplicación de la ley de senos se ha obtenido los valores de:
