El Límite de una Función en una tabla, gráfica y aplicación en el Cálculo Diferencial, ahora lo estudiaremos con más precisión y extensión el concepto de limite y los métodos para calcularlo.
Utilizaremos el ejemplo de la función:
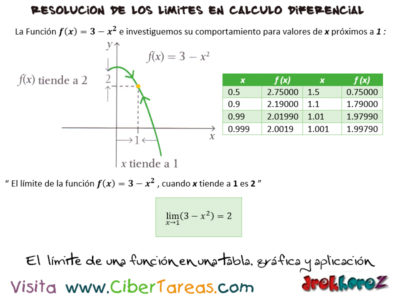
f(x) = 3 – x2
Su comportamiento para los valores de [x] próximos a 1.
Observamos la tabla anterior y la gráfica de la parábola f(x) = 3 -x2 que se muestra en la figura anterior, es fácil concluir que cuando [x] se aproxima a 1 por la izquierda o por la derecha f(x) o hace hacia 2 en dicha situación es expresada:
“El límite de la función f(x) = 3 -x2” cuando [x] tiende a 1 es 2″
Y la expresión simbólica se escribe:
La definición formal de límite en la función f(x) cuando [x] tiende a [a] por la izquierda o por la derecha, es [L] se pueden acercar arbitrariamente los valores f(x) a “L” tanto como deseemos eligiendo una [x] lo bastante cerca de [a] pero no igual a [a] de manera simplificada:
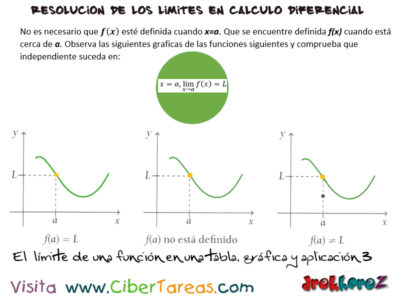
No es necesario que f[x] esté definida cuando [x=a] o cual importa es cómo está definida f(x) cuando [x] está cerca de [a]
Las gráficas de las funciones de las figuras siguientes y comprueba que independiente de lo que suceda en [x=a]: