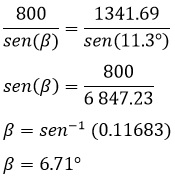Resolución de triángulos oblicuángulos en Matemáticas 2

Para llegar a resolver un triángulo oblicuángulo, consiste en hallar alguno o todos sus elementos a partir de la información disponible, por ejemplo se puede calcular la longitud de uno de sus lados si conoces el valor de los otros dos y el ángulo que determinan

En la vida cotidiana tenemos numerosas situaciones donde se pueden modelarse utilizando triángulos que no necesariamente son rectángulos

Por ejemplo, cuando una avioneta da aviso a la torre de control para efectuar las maniobras de descenso

Para que el aterrizaje sea efectivo, el piloto debe conocer los siguientes datos:

-Punto inicial de la avioneta (P_i) y el final (P_f)

-Longitud de la pista de aterrizaje (d)

-Ángulo de elevación 

Lo anterior desde cualquier punto de la pista de aterrizaje

Ejemplo

-Una pista de aterrizaje tiene 800 m de longitud

-El ángulo de elevación () es de 11.3°

-La distancia que recorre la avioneta desde su punto inicial hasta el final de la pista es de 2,117 m

-En la siguiente figura se puede apreciar la representación gráfica

-Es necesario calcular la distancia x y el ángulo de visión 

Solución

-Datos

P = P_f – P_i = 2117 m

 = 11.3°

d = 800 m

x = ¿?

-Análisis

-Estos datos son necesarios para conocer la distancia del avión al inicio de la pista x y el ángulo de visión () del piloto entre el inicio y el final de la piso de aterrizaje

-Se puede utilizar la ley de cosenos para encontrar x

-La fórmula de la ley de cosenos se expresa de la siguiente forma:

-Ahora se debe sustituir las variables por los valores que nos presenta el ejemplo:

-Posteriormente se aplica la ley de senos, y considerando la igualdad:

-Se aplican las sustituciones para este ejemplo:

-Síntesis interpretativa

-La trayectoria del aterrizaje tiene una longitud de:

1 341.69 m

-El ángulo de visión del piloto entre el inicio y el final de aterrizaje es:

 = 6.71°

-Para resolver un triángulo oblicuángulo, se debe utilizar la ley de senos y la ley de cosenos