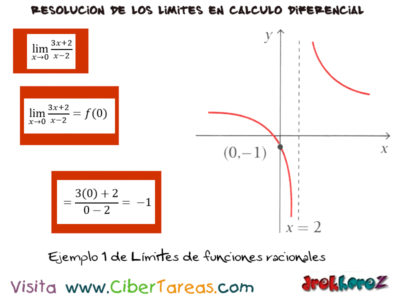
Los Límites de funciones racionales en Cálculo Diferencial, en la forma r(X)=P(x)/q(x) debemos tener en encuentra que r(x) no está definida para q(x)=0 “Recuerda que la división entre entre cero es indefinida”.

Sin embargo en el cálculo de los límites eso puede ser trivial ya que la definición dice que consideremos los valores de x cercanos a (a) pero diferente de (a).

Al calcular la unción no siendo definida para (x=2) sí lo está cerca de 0 observa la gráfica de la siguiente figura.

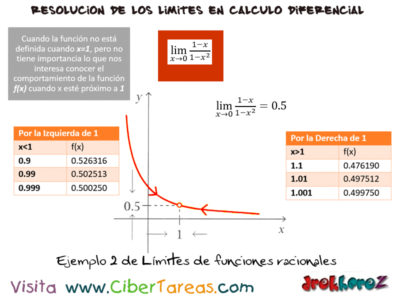
Pero al calcular la función no está definida cuando (x=1) pero no tiene importancia porque lo que nos interesa es conocer el comportamiento de la función f(x) cuando (x) esté próximo a (1). Analiza la siguiente tabla y comprueba que cuando x está próximo a 1 por la izquierda, a gráfica y por la derecha ocurre:

Cuando en la unión racional es posible utilizar una reducción algebraica elemental se puede evitar el valor donde la función no esta definida y así calcularemos el licité directamente.

Al factorizar el denominador como una diferencia de cuadrados tal como en la siguiente imagen:

La función no está definida para (x=2) entonces factorizamos y reducimos la expresión racional.

Al tener presente el trinomio de la forma x²+bx=c es el resultado de multiplicar los binomios (x+m)(x+n) donde m+n=b y mn=c.

Por lo tanto en x²+5x+6 tenemos que b=5 y c=6 luego dos números que sumados de 5 y multiplicados 6 son m y n respectivamente