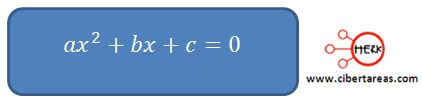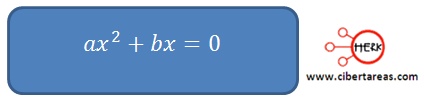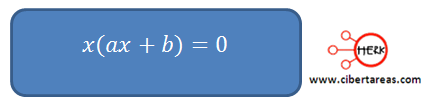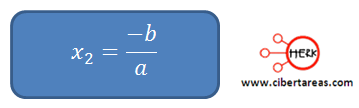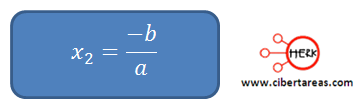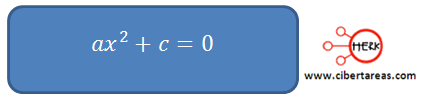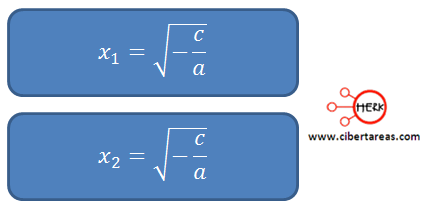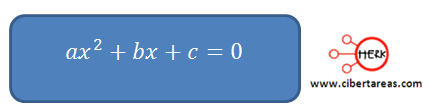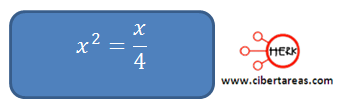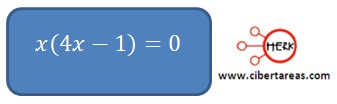Método algebraico de despeje para ecuaciones incompletas – Matemáticas 1
Para poder resolver una ecuación de segundo grado, es mucho mejor presentarla en su forma general, es decir:
De esta manera se identifica fácilmente que el primer miembro de la ecuación es un trinomio general de segundo grado y este puede ser factorizado en dos factores lineales.
Debemos de considerar que no siempre las ecuaciones generales de segundo grado contienen todos sus elementes, en otras palabras no siempre encontraremos un término lineal 2x” o un término constante “c” e incluso podría darse el caso que no existan ambos. Lo que puede ocurrir es que no exista un término cuadrático.
A este tipo de ecuaciones (a las que les falta algún elemento) se les denomina incompletas.
Para estos casos se pude encontrar sus raíces al despejar la variable de interés. Existen tres casos de ecuaciones cuadráticas incompletas:
Caso no. 1 (c=0)
La ecuación:
Se reduce a:
Esta ecuación se puede Factorizar de la siguiente manera:
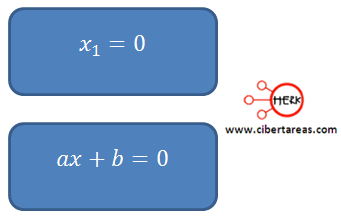
Se obtienen dos ecuaciones igualadas a 0
Al conocer el valor de “x” de la primera ecuación, procedemos a despejar “x” de la segunda ecuación
Caso no. 2 (b=0)
La ecuación:
Se reduce a:
Tenemos que:
Procedemos a despejar en primera instancia la literal x2:
Con esto se obtiene dos raíces cuyos valores son:
Caso no. 3 (b=c=0)
La ecuación:
Se reduce a:
Esto nos indica que ambas raíces serán 0
Veamos el siguiente ejemplo:
Es necesario determinar un número distinto de 0, cuyo cuadrado sea igual a su cuarta parte.
Analicemos la solución:
Se denota por “x” a dicho número, con esto el enunciado se representa de la siguiente manera:
Esta ecuación obtiene una forma equivalente en:
Con esto se puede identificar la que la forma de la ecuación corresponde a la ejemplificación del caso no. 1 antes mencionado, donde la solución es para ecuaciones cuadráticas incompletas.
Vamos a factorizar esta ecuación:
Con esto podremos hallar las dos soluciones:
Este ejemplo plantea una restricción de (x1=0) con esto tenemos que la solución está dada por x2