Método algebraico de determinantes – Matemáticas 1
Se emplea este método cuando las ecuaciones del sistema poseen coeficientes, vamos a considerar el siguiente sistema:
El paso siguiente es aislar los coeficientes de las incógnitas a, b y c en el orden en que aparecen para hallar la solución al sistema
Un método para resolver el sistema de ecuaciones lineales es mediante el cálculo de determinantes (Δ).
En este caso se trabaja con determinantes de la forma (2 x 2), esto se determina porque hay dos elementos en las filas y dos elementos en las columnas.
El resultado se alcanza con una multiplicación cruzada: al primer producto se le resta el segundo
Con esto se obtiene la solución al sistema mediante la relación:
Ejemplo:
El siguiente ejemplo es un sistema, se define los valores de “x” y “y” por el método de determinantes.
En la solución los coeficientes de la primera ecuación son 2, 3, 13 y los coeficientes de la segunda son 4, 1, 11
De donde tenemos los siguientes determinantes organizados en la forma 2×2
Para finalizar el ejemplo se puede resolver el sistema de ecuaciones lineales mediante el cálculo de los determinantes
Con este resultado, encontramos que la solución para el sistema de ecuaciones es el par ordenado (2,3)

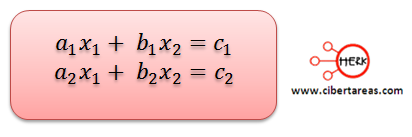
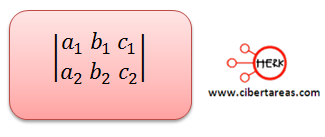


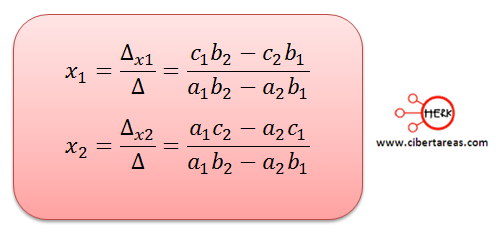
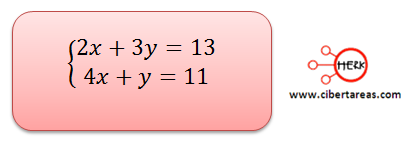

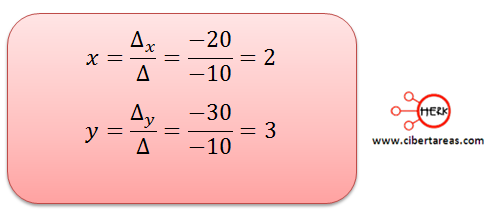

nomada says:
me sirvió la tarea gracias
Sedentario says:
buENA
jonathan says:
gracias <3
VIP says:
de que? XD
silvia daniela gonzalez lopez says:
pss estuvo bueno aunque no ha sido el que lugar de tareas creo que cumple todas la expectativas para el lector …. tiene muy claro los conceptos y son muy conciso en su explicacion .. pero sigo insisitiendo en que es un lugar normal con una tarea normal